What Do All Rectangles Have In Common
Holbox
Mar 25, 2025 · 6 min read
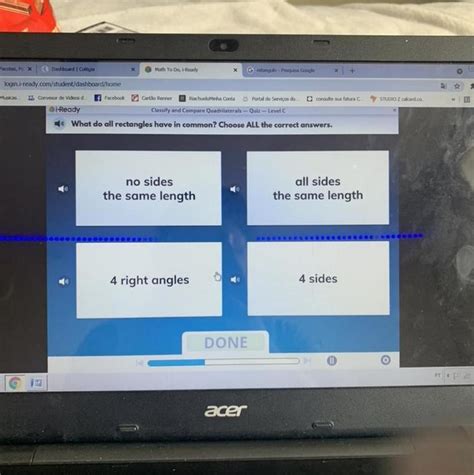
Table of Contents
- What Do All Rectangles Have In Common
- Table of Contents
- What Do All Rectangles Have in Common? A Deep Dive into Quadrilateral Geometry
- The Defining Characteristics of a Rectangle
- 1. Four Right Angles: The Cornerstone of Rectangles
- 2. Opposite Sides are Equal and Parallel: A Perfect Symmetry
- 3. Diagonals Bisect Each Other: A Property of Symmetry
- Rectangles and Their Relationship to Other Quadrilaterals
- 1. Rectangles and Squares: A Special Case
- 2. Rectangles and Parallelograms: A Broader Family
- 3. Rectangles and Rhombuses: Distinct but Related
- 4. Rectangles and Trapezoids: No Overlap
- Beyond the Basics: Exploring Properties and Applications
- 1. Area and Perimeter Calculations: Practical Applications
- 2. Diagonals and their Relationships: Pythagorean Theorem
- 3. Similar Rectangles: Scaling and Proportionality
- 4. Rectangles in Coordinate Geometry: Equations and Graphs
- Rectangles in the Real World: Examples and Applications
- Conclusion: The Enduring Significance of Rectangles
- Latest Posts
- Latest Posts
- Related Post
What Do All Rectangles Have in Common? A Deep Dive into Quadrilateral Geometry
Rectangles. We see them everywhere – in buildings, on screens, in everyday objects. But have you ever stopped to consider what truly unites all rectangles, regardless of their size or proportions? This article will delve into the fundamental properties that define a rectangle, exploring its geometric characteristics, relationships to other quadrilaterals, and even venturing into applications in various fields. We'll uncover the common threads that bind these seemingly diverse shapes into a single, well-defined geometric family.
The Defining Characteristics of a Rectangle
At its core, a rectangle is a quadrilateral, meaning it's a closed two-dimensional shape with four sides. However, being a quadrilateral isn't enough to qualify something as a rectangle. Rectangles possess specific, defining characteristics that distinguish them from other quadrilaterals like squares, parallelograms, rhombuses, and trapezoids. These key properties are:
1. Four Right Angles: The Cornerstone of Rectangles
The most fundamental property of a rectangle is that all four of its interior angles are right angles, each measuring exactly 90 degrees. This is the bedrock upon which all other rectangle properties are built. This consistent angularity is what gives rectangles their distinct, often visually pleasing, shape. Without these right angles, the shape is simply not a rectangle.
2. Opposite Sides are Equal and Parallel: A Perfect Symmetry
Beyond the right angles, rectangles exhibit perfect symmetry in their side lengths. Opposite sides of a rectangle are always equal in length and parallel to each other. This means that if we label the sides of a rectangle as a and b, then the lengths of the parallel sides are consistently a, a, b, and b. This parallelism ensures that the shape maintains its rectangular form, regardless of scaling or rotation.
3. Diagonals Bisect Each Other: A Property of Symmetry
Another crucial characteristic is the behavior of the diagonals. The diagonals of a rectangle bisect each other, meaning they intersect at their midpoints. This intersection point divides each diagonal into two equal segments. This property stems directly from the parallel and equal sides, contributing to the overall symmetry of the rectangle.
Rectangles and Their Relationship to Other Quadrilaterals
Understanding the relationships between rectangles and other quadrilaterals helps clarify the unique properties of rectangles within the broader context of quadrilateral geometry.
1. Rectangles and Squares: A Special Case
A square is a special type of rectangle. It fulfills all the criteria of a rectangle – four right angles, opposite sides equal and parallel, diagonals bisecting each other – with the added condition that all four sides are equal in length. Essentially, a square is a rectangle with the extra constraint of equal side lengths.
2. Rectangles and Parallelograms: A Broader Family
A parallelogram is a quadrilateral with opposite sides parallel. Rectangles are a subset of parallelograms. All rectangles are parallelograms, but not all parallelograms are rectangles. The key difference is the presence of right angles. Parallelograms can have angles of varying measures, whereas rectangles are characterized by their exclusive 90-degree angles.
3. Rectangles and Rhombuses: Distinct but Related
A rhombus is a quadrilateral with all four sides equal in length. While a rhombus has parallel opposite sides (making it a parallelogram), it does not necessarily have right angles. Therefore, a rhombus and a rectangle are distinct shapes, although a square, as mentioned earlier, serves as the intersection of both sets.
4. Rectangles and Trapezoids: No Overlap
A trapezoid (or trapezium) is a quadrilateral with at least one pair of parallel sides. Rectangles, possessing two pairs of parallel sides, are fundamentally different from trapezoids. They share no overlapping properties except for being quadrilaterals. Trapezoids lack the consistent right angles and equal opposite sides that define rectangles.
Beyond the Basics: Exploring Properties and Applications
The fundamental properties discussed above lay the foundation for more advanced geometric concepts related to rectangles.
1. Area and Perimeter Calculations: Practical Applications
Calculating the area and perimeter of a rectangle is a cornerstone of elementary geometry. The area (A) is simply the product of its length (l) and width (w): A = l * w. The perimeter (P), the total length of its sides, is given by P = 2l + 2w. These formulas have countless practical applications in fields like construction, design, and manufacturing. From calculating the amount of paint needed for a wall to determining the length of fencing required for a yard, the area and perimeter of rectangles are essential calculations.
2. Diagonals and their Relationships: Pythagorean Theorem
The diagonals of a rectangle are related to its sides through the Pythagorean theorem. If we consider a rectangle with sides a and b, and a diagonal d, then the theorem states: d² = a² + b². This relationship allows us to calculate the length of the diagonal given the side lengths, and vice versa. This has significant applications in various fields, including surveying and navigation.
3. Similar Rectangles: Scaling and Proportionality
Two rectangles are considered similar if their corresponding angles are equal (which is always true for rectangles) and their corresponding sides are proportional. This means that one rectangle is essentially a scaled version of the other. The concept of similar rectangles is critical in fields like cartography (map-making) and architectural modeling, where scaled representations of real-world objects are frequently used.
4. Rectangles in Coordinate Geometry: Equations and Graphs
In coordinate geometry, rectangles can be represented using equations and graphs. For instance, a rectangle with vertices at (0,0), (a,0), (a,b), and (0,b) can be described by inequalities involving x and y coordinates. Understanding this representation is crucial for various applications in computer graphics, game development, and other areas where graphical representation is necessary.
Rectangles in the Real World: Examples and Applications
The ubiquitous nature of rectangles is evident in countless applications across diverse fields:
-
Architecture and Construction: Buildings, rooms, windows, doors – all frequently based on rectangular designs for structural integrity, efficiency, and aesthetics.
-
Engineering and Manufacturing: Machine parts, electronic components, and various manufactured goods often have rectangular shapes for ease of production and assembly.
-
Graphic Design and Art: Rectangles are fundamental building blocks in visual design, used to create layouts, frames, and compositional elements in posters, websites, and various artworks.
-
Everyday Objects: Books, screens, tables, and countless other objects are rectangular in shape, showcasing the practical adaptability of the rectangle in everyday life.
-
Computer Science and Programming: Rectangles are central to computer graphics, representing objects and regions on screens and in digital environments.
Conclusion: The Enduring Significance of Rectangles
In conclusion, while seemingly simple, rectangles possess a rich set of geometric properties that unify their diverse appearances. From their defining right angles and parallel sides to the relationships between their diagonals and the applications of the Pythagorean theorem, rectangles hold a special place in geometry. Their consistent characteristics make them incredibly versatile and practical, contributing to their widespread presence in both the natural and man-made worlds. Understanding these properties isn't just an exercise in abstract geometry; it's a key to comprehending the shapes that surround us and the mathematical principles that govern them. The next time you see a rectangle, remember the underlying geometric principles that define its form and functionality. It's a testament to the enduring power and elegance of mathematical structures in shaping our world.
Latest Posts
Latest Posts
-
According To Federal Regulations The Expedited Review Process
Mar 29, 2025
-
Which Of The Following Is True About Database Rows
Mar 29, 2025
-
Steam Flows Steadily Through An Adiabatic Turbine
Mar 29, 2025
-
Which Statement Correctly Describes The Initiative Versus Guilt Stage
Mar 29, 2025
-
Cash Flows From Investing Do Not Include Cash Flows From
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about What Do All Rectangles Have In Common . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
