The Rectangular Homogeneous Gate Shown Below Is
Holbox
Mar 27, 2025 · 6 min read
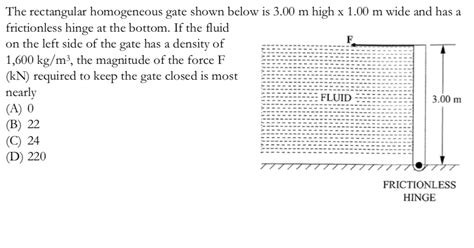
Table of Contents
- The Rectangular Homogeneous Gate Shown Below Is
- Table of Contents
- Analyzing the Rectangular Homogeneous Gate: Equilibrium, Forces, and Applications
- Understanding the System: Defining the Parameters
- Hydrostatic Pressure: The Force of the Fluid
- Calculating the Hydrostatic Force
- Locating the Center of Pressure
- The Weight of the Gate: A Significant Factor
- Achieving Equilibrium: Balancing Forces and Moments
- Practical Applications and Examples
- Advanced Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Analyzing the Rectangular Homogeneous Gate: Equilibrium, Forces, and Applications
The analysis of a rectangular homogeneous gate, often encountered in engineering and physics problems, provides a fundamental understanding of static equilibrium, fluid pressure, and the principles governing submerged structures. This article delves deep into the mechanics of such a gate, exploring its behavior under various conditions, the forces acting upon it, and its practical applications in various engineering disciplines.
Understanding the System: Defining the Parameters
Before we begin our analysis, let's define the key parameters characterizing our rectangular homogeneous gate:
-
Dimensions: The gate possesses a rectangular shape with width (w) and height (h). These dimensions are crucial for calculating the area and subsequently, the forces acting on the gate.
-
Density: The gate is assumed to be homogeneous, meaning its density (ρ<sub>gate</sub>) is uniform throughout. This simplifies the calculation of the gate's weight and center of gravity.
-
Fluid Properties: The gate is submerged in a fluid, typically water, characterized by its density (ρ<sub>fluid</sub>) and the acceleration due to gravity (g). The fluid's density determines the hydrostatic pressure exerted on the gate.
-
Hinge/Pivot Point: The gate is typically hinged or pivoted at a specific point, which we'll denote as the pivot point. The location of this point is critical in determining the forces and moments required to maintain equilibrium.
-
Submergence Depth: The depth to which the gate is submerged significantly influences the hydrostatic pressure acting on it. This depth will be denoted as 'd'.
Hydrostatic Pressure: The Force of the Fluid
The fundamental force acting on the submerged rectangular gate is the hydrostatic pressure exerted by the fluid. This pressure is not uniform but increases linearly with depth. The pressure at any point at depth 'y' below the fluid surface is given by:
P(y) = ρ<sub>fluid</sub> * g * y
This pressure acts perpendicularly to the surface of the gate. To find the total hydrostatic force acting on the gate, we need to integrate this pressure over the submerged area of the gate.
Calculating the Hydrostatic Force
The total hydrostatic force (F<sub>hydro</sub>) acting on the rectangular gate can be calculated by integrating the pressure over the submerged area:
F<sub>hydro</sub> = ∫ P(y) dA
Where 'dA' represents an infinitesimal area element. For a rectangular gate, this integration simplifies to:
F<sub>hydro</sub> = ρ<sub>fluid</sub> * g * w * ∫ y dy (integration is done over the submerged height)
This results in:
F<sub>hydro</sub> = ρ<sub>fluid</sub> * g * w * (h<sub>submerged</sub>²/2)
Where h<sub>submerged</sub> is the height of the gate submerged in the fluid.
Locating the Center of Pressure
The hydrostatic force doesn't act at the geometric center of the submerged area. Instead, it acts at a point called the center of pressure. The location of the center of pressure (y<sub>cp</sub>) is given by:
y<sub>cp</sub> = (2/3) * h<sub>submerged</sub>
This is measured from the surface of the fluid.
The Weight of the Gate: A Significant Factor
The weight of the gate (W<sub>gate</sub>) also plays a critical role in its equilibrium. The weight is given by:
W<sub>gate</sub> = ρ<sub>gate</sub> * V<sub>gate</sub> * g
Where V<sub>gate</sub> is the volume of the gate, equal to w * h * thickness (t). This weight acts vertically downwards through the gate's center of gravity, which is located at the geometric center of the rectangle for a homogeneous gate:
y<sub>cg</sub> = h/2
Achieving Equilibrium: Balancing Forces and Moments
For the gate to remain in equilibrium, the sum of the forces and the sum of the moments about any point must be zero. This equilibrium condition provides the equations needed to solve for unknown forces or parameters in the system.
Let's consider moments about the pivot point:
ΣM<sub>pivot</sub> = 0
This equation involves the moments due to the hydrostatic force (F<sub>hydro</sub>), the weight of the gate (W<sub>gate</sub>), and any other external forces acting on the gate. The distance of each force's line of action from the pivot point is crucial in calculating the moment.
Practical Applications and Examples
The analysis of a rectangular homogeneous gate has wide-ranging applications in various engineering fields:
-
Dam Design: Understanding the forces acting on dam gates is essential for ensuring structural stability and preventing failure. The principles discussed here are fundamental to designing and analyzing dam gates of various shapes and sizes. Precise calculations of hydrostatic pressure and resulting forces are critical for the safety and longevity of such structures.
-
Flood Control Structures: Gates used in flood control systems need to withstand significant hydrostatic forces. The analysis enables engineers to determine the optimal size and strength of these gates to effectively manage water flow during flood events.
-
Water Storage Tanks: Gates used in water storage tanks must be designed to withstand the pressure of the contained water. Accurate analysis is crucial for ensuring the integrity of the tank and preventing leaks or structural failure.
-
Hydraulic Systems: Rectangular gates are often employed in hydraulic systems to control the flow of fluids. Understanding their behavior under pressure is crucial for efficient and safe operation.
-
Submarine Door Design: The principles of hydrostatic pressure and equilibrium are directly applicable in designing and analyzing submarine doors, which need to withstand immense external water pressure.
Advanced Considerations
The analysis presented above simplifies some aspects for clarity. More complex scenarios involve:
-
Non-homogeneous Gates: If the gate is not homogeneous, the center of gravity will shift, requiring a more detailed calculation of the weight's moment.
-
Multiple Fluids: If the gate is submerged in multiple fluids with different densities, the hydrostatic pressure calculation becomes more complex, requiring integration across each fluid layer.
-
Dynamic Loading: This analysis focuses on static equilibrium. Dynamic loading, such as waves or fluctuating water levels, adds complexity and necessitates more advanced techniques for accurate analysis.
-
Friction at the Hinge: Friction at the pivot point can influence the equilibrium condition and requires additional considerations in the force and moment balance equations.
Conclusion
The analysis of a rectangular homogeneous gate provides a fundamental understanding of static equilibrium and the interaction between submerged structures and fluids. By carefully considering the hydrostatic pressure, the gate's weight, and the location of the pivot point, engineers can accurately determine the forces acting on the gate and design it to withstand these forces safely and effectively. Understanding these principles is vital across various engineering disciplines, from dam construction to hydraulic systems and beyond. The concepts detailed above serve as a foundation for more complex analyses involving non-homogeneous gates, dynamic loading, and other real-world conditions. This thorough understanding ensures the safety, reliability, and efficiency of numerous engineering structures and systems.
Latest Posts
Latest Posts
-
A Game Is Said To Be Fair If
Mar 31, 2025
-
Which Of The Following Is The Strongest Acid
Mar 31, 2025
-
Please Label The Circular Flow Diagram
Mar 31, 2025
-
Identify True Statements About The Si Unit Of Force
Mar 31, 2025
-
All Of The Following Are True About Sql Except
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about The Rectangular Homogeneous Gate Shown Below Is . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
