Suppose T And Z Are Random Variables.
Holbox
Mar 20, 2025 · 6 min read
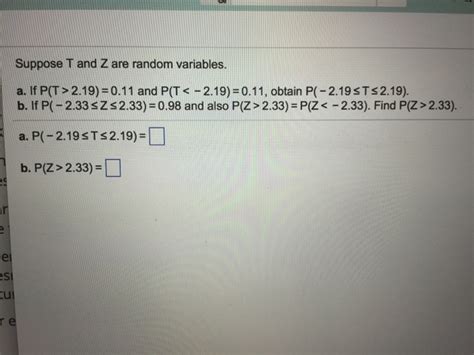
Table of Contents
Suppose T and Z are Random Variables: A Deep Dive into Joint Distributions, Covariance, and Independence
Understanding the relationship between two random variables is crucial in many fields, from statistics and probability to machine learning and finance. This article delves into the intricacies of working with two random variables, T and Z, exploring their joint distribution, covariance, correlation, and importantly, the concept of independence. We'll cover various aspects, providing examples and explanations to solidify your understanding.
Defining Random Variables T and Z
Before diving into the complexities of their relationship, let's establish what we mean by random variables T and Z. A random variable is a variable whose value is a numerical outcome of a random phenomenon. It's a function that maps outcomes from a sample space to numerical values. T and Z could represent anything from the height and weight of individuals in a population to the temperature and humidity in a specific location at a given time. The nature of these variables – whether discrete (taking on distinct values) or continuous (taking on values within a range) – significantly impacts how we analyze their relationship.
Joint Probability Distribution: The Foundation
The relationship between T and Z is fundamentally described by their joint probability distribution. This distribution specifies the probability that T takes on a particular value and simultaneously Z takes on another particular value. We denote this as P(T=t, Z=z) for discrete random variables and f<sub>T,Z</sub>(t,z) for continuous random variables (where f represents the joint probability density function).
Discrete Random Variables: The Joint Probability Mass Function (PMF)
For discrete random variables, the joint PMF is a table or function that lists the probability of each possible combination of values for T and Z. Consider the following example:
| T \ Z | 0 | 1 | 2 |
|---|---|---|---|
| 0 | 0.1 | 0.2 | 0.1 |
| 1 | 0.2 | 0.3 | 0.1 |
This table shows the joint PMF. For instance, P(T=0, Z=1) = 0.2. The sum of all probabilities in the table must equal 1.
Continuous Random Variables: The Joint Probability Density Function (PDF)
For continuous random variables, the joint PDF, f<sub>T,Z</sub>(t,z), describes the probability density at each point (t,z) in the two-dimensional space. The probability that T and Z fall within a specific region is obtained by integrating the joint PDF over that region:
P(a ≤ T ≤ b, c ≤ Z ≤ d) = ∫<sub>c</sub><sup>d</sup> ∫<sub>a</sub><sup>b</sup> f<sub>T,Z</sub>(t,z) dt dz
Marginal Distributions: Individual Behaviors
From the joint distribution, we can derive the marginal distributions of T and Z. These distributions describe the probability of each variable independently of the other.
-
Marginal distribution of T: For discrete variables, this is P(T=t) = Σ<sub>z</sub> P(T=t, Z=z). For continuous variables, it's f<sub>T</sub>(t) = ∫ f<sub>T,Z</sub>(t,z) dz (integrating over all possible values of Z).
-
Marginal distribution of Z: Similarly, for discrete variables, this is P(Z=z) = Σ<sub>t</sub> P(T=t, Z=z), and for continuous variables, f<sub>Z</sub>(z) = ∫ f<sub>T,Z</sub>(t,z) dt (integrating over all possible values of T).
Conditional Distributions: Dependence Unveiled
The conditional distribution of one variable given the other reveals how the probability of one variable changes based on the value of the other.
-
Conditional distribution of T given Z: P(T=t | Z=z) = P(T=t, Z=z) / P(Z=z) for discrete variables, and f<sub>T|Z</sub>(t|z) = f<sub>T,Z</sub>(t,z) / f<sub>Z</sub>(z) for continuous variables.
-
Conditional distribution of Z given T: Similarly, P(Z=z | T=t) = P(T=t, Z=z) / P(T=t) and f<sub>Z|T</sub>(z|t) = f<sub>T,Z</sub>(t,z) / f<sub>T</sub>(t).
Covariance and Correlation: Measuring Linear Dependence
Covariance and correlation quantify the linear relationship between T and Z. A positive value indicates a positive relationship (when one increases, the other tends to increase), a negative value indicates a negative relationship, and a value close to zero suggests weak or no linear relationship.
Covariance (Cov(T,Z)): This measures the direction and strength of the linear relationship. For continuous random variables:
Cov(T,Z) = E[(T - E[T])(Z - E[Z])] = E[TZ] - E[T]E[Z]
where E[.] denotes the expected value. A similar formula applies to discrete variables, using summation instead of integration.
Correlation (Corr(T,Z)): This is a standardized measure of the linear relationship, ranging from -1 to +1. It's calculated as:
Corr(T,Z) = Cov(T,Z) / (σ<sub>T</sub>σ<sub>Z</sub>)
where σ<sub>T</sub> and σ<sub>Z</sub> are the standard deviations of T and Z, respectively. A correlation of +1 indicates a perfect positive linear relationship, -1 a perfect negative linear relationship, and 0 no linear relationship. It's crucial to remember that correlation does not imply causation.
Independence: The Absence of Relationship
Two random variables T and Z are independent if the occurrence of one event does not affect the probability of the other. This means:
- For discrete variables: P(T=t, Z=z) = P(T=t)P(Z=z) for all t and z.
- For continuous variables: f<sub>T,Z</sub>(t,z) = f<sub>T</sub>(t)f<sub>Z</sub>(z) for all t and z.
Independence implies zero covariance and zero correlation. However, the converse is not true: zero covariance or correlation does not necessarily imply independence. This is because covariance and correlation only capture linear dependence. Non-linear relationships can exist even if the covariance and correlation are zero.
Examples and Applications
Let's illustrate these concepts with some examples:
Example 1: Height and Weight
Consider height (T) and weight (Z) of individuals. We'd expect a positive covariance and correlation, indicating taller people tend to weigh more. However, the relationship is not perfect; there will be variation.
Example 2: Temperature and Ice Cream Sales
Temperature (T) and daily ice cream sales (Z) likely have a positive correlation. Higher temperatures tend to lead to increased ice cream sales. This is a real-world example of a strong correlation.
Example 3: Coin Tosses
The outcome of two consecutive coin tosses (T and Z) are independent events. The outcome of the first toss does not influence the probability of the second toss. Their joint distribution is simply the product of their individual probabilities.
Advanced Topics
Further exploration into the relationship between T and Z could involve:
- Conditional expectation: E[T|Z] – the expected value of T given a specific value of Z.
- Regression analysis: Modeling the relationship between T and Z using regression techniques.
- Copulas: Modeling the dependence structure between T and Z beyond linear relationships.
- Multivariate distributions: Extending these concepts to more than two random variables.
Conclusion
Understanding the relationship between two random variables, T and Z, is a fundamental concept in probability and statistics. This article provided a comprehensive overview of joint distributions, marginal distributions, conditional distributions, covariance, correlation, and independence. By mastering these concepts, you gain a powerful toolkit for analyzing data and drawing meaningful inferences about the world around us. Remember that while correlation can highlight potential relationships, further investigation is crucial to establish causation. The application of these concepts extends far beyond theoretical statistics, permeating diverse fields requiring probabilistic modeling and data analysis. Continue exploring these topics to unlock a deeper understanding of randomness and its implications.
Latest Posts
Latest Posts
-
A Business Disability Buyout Plan Policy Is Designed
Mar 27, 2025
-
Flattened Membranous Sacs That Modify And Package A Secretion
Mar 27, 2025
-
Discounting Is The Opposite Of
Mar 27, 2025
-
The Reaction Of A Certain Alcohol With Hbr
Mar 27, 2025
-
Which Of The Following Is A Service
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Suppose T And Z Are Random Variables. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
