Match The Function With Its Graph Labeled I Vi
Holbox
Mar 27, 2025 · 6 min read
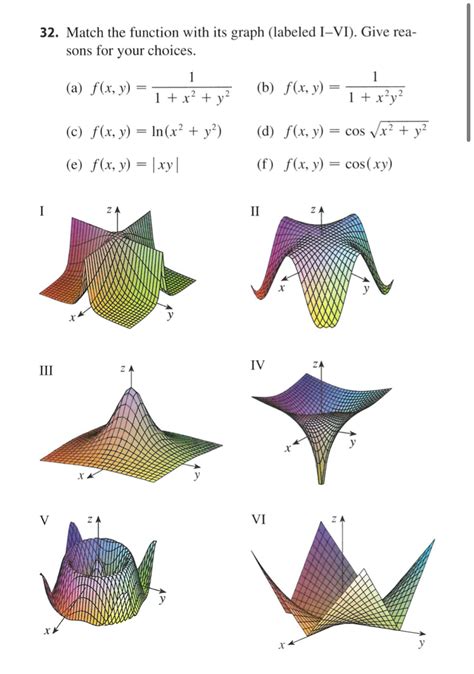
Table of Contents
- Match The Function With Its Graph Labeled I Vi
- Table of Contents
- Matching Functions to Their Graphs: A Comprehensive Guide
- Understanding Function Families
- 1. Linear Functions (f(x) = mx + b)
- 2. Quadratic Functions (f(x) = ax² + bx + c)
- 3. Cubic Functions (f(x) = ax³ + bx² + cx + d)
- 4. Polynomial Functions (f(x) = a_nxⁿ + a_(n-1)x^(n-1) + ... + a₁x + a₀)
- 5. Rational Functions (f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials)
- 6. Exponential Functions (f(x) = aᵇˣ)
- 7. Logarithmic Functions (f(x) = log_b(x))
- 8. Trigonometric Functions (sine, cosine, tangent, etc.)
- Strategies for Matching Functions and Graphs
- 1. Identify Key Features
- 2. Use Process of Elimination
- 3. Analyze the Domain and Range
- 4. Consider the Leading Coefficient and Degree (for Polynomials)
- 5. Test Points
- 6. Utilize Technology (Graphing Calculators or Software)
- Example Problem: Matching Six Functions to Their Graphs (Labeled I - VI)
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Matching Functions to Their Graphs: A Comprehensive Guide
Matching functions to their graphs is a fundamental skill in mathematics, particularly in algebra, calculus, and pre-calculus. This ability allows you to visualize the behavior of a function and understand its properties, such as its domain, range, intercepts, asymptotes, and symmetry. This comprehensive guide will walk you through various techniques to effectively match functions to their graphs, covering a broad range of function types, from simple linear equations to more complex trigonometric and exponential functions. We will use a problem-solving approach, employing visual analysis, key features identification, and strategic elimination.
Understanding Function Families
Before diving into specific examples, let's establish a solid foundation by reviewing key function families and their characteristic graph shapes. Recognizing these patterns is crucial for efficient graph-function matching.
1. Linear Functions (f(x) = mx + b)
- Characteristics: Straight lines with a constant slope (m). 'b' represents the y-intercept (where the line crosses the y-axis). A positive slope indicates an increasing function, while a negative slope indicates a decreasing function.
- Visual Cue: A straight line, either increasing or decreasing.
2. Quadratic Functions (f(x) = ax² + bx + c)
- Characteristics: Parabolic curves. The coefficient 'a' determines the direction of the parabola (opens upwards if a > 0, downwards if a < 0). The vertex represents the minimum or maximum value of the function.
- Visual Cue: A U-shaped curve (parabola), opening upwards or downwards.
3. Cubic Functions (f(x) = ax³ + bx² + cx + d)
- Characteristics: Typically S-shaped curves. They can have up to two turning points (local maxima or minima). The leading coefficient 'a' determines the end behavior (as x approaches positive or negative infinity).
- Visual Cue: An S-shaped curve with potential turning points.
4. Polynomial Functions (f(x) = a_nxⁿ + a_(n-1)x^(n-1) + ... + a₁x + a₀)
- Characteristics: Smooth, continuous curves with varying numbers of turning points depending on the degree (highest power of x). The end behavior is determined by the leading coefficient and degree.
- Visual Cue: Smooth curves with potential multiple turning points. The end behavior will provide strong clues.
5. Rational Functions (f(x) = P(x) / Q(x), where P(x) and Q(x) are polynomials)
- Characteristics: May have asymptotes (vertical, horizontal, or slant). Asymptotes are lines that the graph approaches but never touches. They can have discontinuities (holes or jumps).
- Visual Cue: Curves with potential vertical, horizontal, or slant asymptotes. Discontinuities are also common.
6. Exponential Functions (f(x) = aᵇˣ)
- Characteristics: Rapidly increasing or decreasing curves. The base 'b' determines the rate of growth or decay. If b > 1, the function is increasing; if 0 < b < 1, the function is decreasing. They have a horizontal asymptote at y = 0.
- Visual Cue: A curve that approaches a horizontal asymptote (typically the x-axis).
7. Logarithmic Functions (f(x) = log_b(x))
- Characteristics: The inverse of exponential functions. They have a vertical asymptote at x = 0. They increase slowly as x increases.
- Visual Cue: A curve that approaches a vertical asymptote (typically the y-axis).
8. Trigonometric Functions (sine, cosine, tangent, etc.)
- Characteristics: Periodic functions that repeat their values over a certain interval (period). Sine and cosine have a range between -1 and 1, while tangent has vertical asymptotes.
- Visual Cue: Repeating waves (sine and cosine) or curves with vertical asymptotes (tangent).
Strategies for Matching Functions and Graphs
Now that we have reviewed the basic function families, let's explore effective strategies to match functions to their graphs.
1. Identify Key Features
Start by identifying key features of the given functions:
- Intercepts: Where the graph crosses the x-axis (x-intercepts) and the y-axis (y-intercept).
- Asymptotes: Vertical, horizontal, or slant lines that the graph approaches but never touches.
- Symmetry: Is the graph symmetric about the y-axis (even function), the origin (odd function), or neither?
- Turning Points: Local maxima or minima where the graph changes direction.
- End Behavior: What happens to the function values as x approaches positive and negative infinity?
2. Use Process of Elimination
Once you've identified key features, start eliminating graphs that don't match. For instance, if a function has a vertical asymptote, you can eliminate any graphs without such an asymptote.
3. Analyze the Domain and Range
The domain is the set of all possible x-values, and the range is the set of all possible y-values. Consider whether the domain or range is restricted in any way. For example, logarithmic functions have a restricted domain (x > 0), while square root functions have a restricted domain (radicand ≥ 0).
4. Consider the Leading Coefficient and Degree (for Polynomials)
For polynomial functions, the leading coefficient and degree provide valuable clues about the end behavior and the number of potential turning points.
5. Test Points
If you're still unsure, you can test specific points to see if they satisfy the function. Substitute a few x-values into the function and check if the corresponding y-values match the graph.
6. Utilize Technology (Graphing Calculators or Software)
Graphing calculators or software can be valuable tools to visually verify your matches. However, it is crucial to first understand the analytical methods. Technology should be used for confirmation, not as a primary tool for solving the problem.
Example Problem: Matching Six Functions to Their Graphs (Labeled I - VI)
Let's assume we have the following six functions:
I. f(x) = x² - 4x + 3 II. f(x) = 2ˣ III. f(x) = -x³ + 2x IV. f(x) = 1/(x - 2) V. f(x) = sin(x) VI. f(x) = ln(x)
(Note: Imagine six graphs labeled I to VI are presented here. For the purpose of this text-based example, we'll describe the characteristics of the graphs instead of providing actual images.)
Analysis:
-
I. f(x) = x² - 4x + 3: This is a quadratic function. Its graph would be a parabola opening upwards (since the coefficient of x² is positive). Find the vertex and intercepts to pinpoint its location.
-
II. f(x) = 2ˣ: This is an exponential function. Its graph would be an increasing curve approaching a horizontal asymptote at y = 0.
-
III. f(x) = -x³ + 2x: This is a cubic function. Its graph would be an S-shaped curve, likely decreasing as x goes to positive infinity and increasing as x goes to negative infinity (due to the negative leading coefficient).
-
IV. f(x) = 1/(x - 2): This is a rational function. It will have a vertical asymptote at x = 2 and a horizontal asymptote at y = 0.
-
V. f(x) = sin(x): This is a trigonometric function. Its graph would be a wave oscillating between -1 and 1.
-
VI. f(x) = ln(x): This is a logarithmic function. Its graph would be increasing, approaching a vertical asymptote at x = 0.
Matching: By analyzing the key features of each function, you should be able to match them to the corresponding graphs (I-VI). For instance, the graph exhibiting a wave pattern would undoubtedly correspond to the sine function (V). Similarly, the graph showing a vertical asymptote would likely correspond to the rational function (IV).
Conclusion
Matching functions to their graphs is a multifaceted skill that requires a firm understanding of function families, their properties, and strategic analytical techniques. This involves recognizing key features such as intercepts, asymptotes, symmetry, turning points, and end behavior. By mastering these techniques and practicing regularly, you'll develop a strong intuition for visualizing functions and interpreting their graphical representations. Remember to combine analytical skills with visual inspection for a thorough and accurate matching process. This approach will not only improve your problem-solving skills but also enhance your understanding of the underlying mathematical concepts.
Latest Posts
Latest Posts
-
The Invisible Hand Refers To The
Mar 31, 2025
-
The Master Budgeting Process Begins With The
Mar 31, 2025
-
Everyones An Author 4th Edition Pdf
Mar 31, 2025
-
Match Each Erythrocyte Disorder To Its Cause Or Definition
Mar 31, 2025
-
Label The Veins Of The Head And Neck
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Match The Function With Its Graph Labeled I Vi . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
