Differentiate Y Sec θ Tan θ
Holbox
Mar 21, 2025 · 4 min read
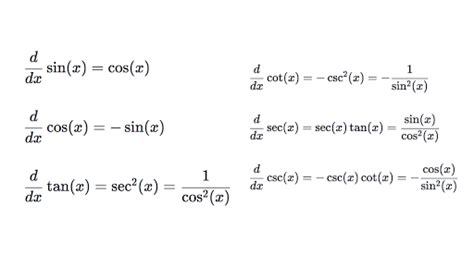
Table of Contents
- Differentiate Y Sec θ Tan θ
- Table of Contents
- Differentiating y = sec θ tan θ: A Comprehensive Guide
- Understanding the Components: sec θ and tan θ
- Secant (sec θ)
- Tangent (tan θ)
- Differentiating y = sec θ tan θ: Methods and Explanations
- The Product Rule
- Applying the Product Rule
- Alternative Approach: Using Trigonometric Identities
- Practical Examples and Applications
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Differentiating y = sec θ tan θ: A Comprehensive Guide
This article provides a detailed explanation of how to differentiate the trigonometric function y = sec θ tan θ. We'll explore various approaches, delve into the underlying principles, and offer practical examples to solidify your understanding. Understanding this differentiation is crucial for various applications in calculus and related fields.
Understanding the Components: sec θ and tan θ
Before differentiating y = sec θ tan θ, let's refresh our understanding of the individual components: sec θ and tan θ.
Secant (sec θ)
The secant function (sec θ) is the reciprocal of the cosine function (cos θ):
sec θ = 1 / cos θ
Its derivative is:
d(sec θ)/dθ = sec θ tan θ
This derivative is a fundamental result you should commit to memory. It's derived using the quotient rule, which we'll revisit later in the context of differentiating the entire function.
Tangent (tan θ)
The tangent function (tan θ) is the ratio of the sine function (sin θ) to the cosine function (cos θ):
tan θ = sin θ / cos θ
Its derivative is:
d(tan θ)/dθ = sec² θ
Again, this is a crucial derivative to remember, readily derived using the quotient rule.
Differentiating y = sec θ tan θ: Methods and Explanations
Now, let's tackle the differentiation of y = sec θ tan θ. We'll employ the product rule, a cornerstone of differential calculus.
The Product Rule
The product rule states that the derivative of a product of two functions, u(θ) and v(θ), is given by:
d(uv)/dθ = u(dv/dθ) + v(du/dθ)
In our case, u(θ) = sec θ and v(θ) = tan θ.
Applying the Product Rule
-
Identify u(θ) and v(θ):
- u(θ) = sec θ
- v(θ) = tan θ
-
Find the derivatives:
- du/dθ = sec θ tan θ (derivative of sec θ)
- dv/dθ = sec² θ (derivative of tan θ)
-
Apply the product rule formula:
dy/dθ = sec θ (sec² θ) + tan θ (sec θ tan θ)
-
Simplify the expression:
dy/dθ = sec³ θ + sec θ tan² θ
We can further simplify this by factoring out sec θ:
dy/dθ = sec θ (sec² θ + tan² θ)
This is the final derivative of y = sec θ tan θ. Note that we've used the previously established derivatives of sec θ and tan θ.
Alternative Approach: Using Trigonometric Identities
We can also approach this problem by first expressing sec θ and tan θ in terms of sine and cosine, then applying the product rule and simplifying using trigonometric identities.
-
Rewrite in terms of sine and cosine:
y = (1/cos θ)(sin θ/cos θ) = sin θ / cos² θ
-
Apply the quotient rule:
The quotient rule states that the derivative of f(x)/g(x) is:
[g(x)f'(x) - f(x)g'(x)] / [g(x)]²
In our case: f(θ) = sin θ and g(θ) = cos² θ
Therefore:
dy/dθ = [cos²θ(cosθ) - sinθ(2cosθ)(-sinθ)] / (cos²θ)²
- Simplify:
dy/dθ = [cos³θ + 2sin²θcosθ] / cos⁴θ
dy/dθ = cos³θ/cos⁴θ + 2sin²θcosθ/cos⁴θ
dy/dθ = 1/cosθ + 2sin²θ/cos³θ
- Convert back to sec θ and tan θ:
dy/dθ = sec θ + 2(tan²θ)/cos θ
dy/dθ = sec θ + 2(tan²θ)sec θ
dy/dθ = sec θ (1 + 2tan²θ)
While this approach is valid, it's generally more cumbersome than using the product rule directly with the sec θ and tan θ forms. The final result might seem different at first glance, but with some trigonometric manipulation (specifically using the Pythagorean identity 1 + tan²θ = sec²θ), you can show that this expression is equivalent to sec θ (sec²θ + tan²θ).
Practical Examples and Applications
Let's consider a few examples to illustrate the application of the derivative.
Example 1:
Find the slope of the tangent line to the curve y = sec θ tan θ at θ = π/4.
First, we evaluate the derivative at θ = π/4:
dy/dθ = sec θ (sec² θ + tan² θ)
At θ = π/4:
sec(π/4) = √2 tan(π/4) = 1
dy/dθ = √2 ( (√2)² + 1²) = √2 (2 + 1) = 3√2
Therefore, the slope of the tangent line at θ = π/4 is 3√2.
Example 2:
Find the equation of the tangent line to the curve y = sec θ tan θ at θ = π/3.
Follow the same procedure as in Example 1: first calculate the derivative at θ = π/3, then use the point-slope form of a line (y - y₁ = m(θ - θ₁)) to find the equation of the tangent line.
Conclusion
Differentiating y = sec θ tan θ involves a straightforward application of the product rule, utilizing the known derivatives of sec θ and tan θ. While alternative methods exist, utilizing the product rule directly is generally the most efficient approach. Mastering this differentiation is crucial for a deeper understanding of calculus and its application in various fields including physics, engineering, and computer science. Remember to practice different variations and examples to solidify your understanding and skill. The more you practice, the more comfortable and confident you'll become with differentiating complex trigonometric functions.
Latest Posts
Latest Posts
-
Art Labeling Activity Basic Anatomy Of The Skin
Mar 28, 2025
-
As Organic Vegetables Increase In Popularity
Mar 28, 2025
-
The Highest Barrier That A Projectile Can Clear Is
Mar 28, 2025
-
Which Statement Is True Regarding Venipuncture Procedures In Mice
Mar 28, 2025
-
At The End Of Mitosis The Daughter Cells Are
Mar 28, 2025
Related Post
Thank you for visiting our website which covers about Differentiate Y Sec θ Tan θ . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
