You Charge An Initially Uncharged Capacitor Through Resistor
Holbox
Mar 24, 2025 · 6 min read
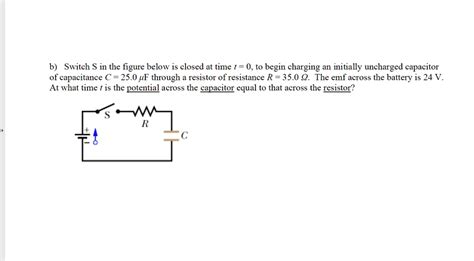
Table of Contents
- You Charge An Initially Uncharged Capacitor Through Resistor
- Table of Contents
- Charging an Initially Uncharged Capacitor Through a Resistor: A Comprehensive Guide
- The RC Circuit: The Heart of the Matter
- Understanding the Components
- The Charging Process: An Exponential Rise
- The Time Constant (τ = RC): A Crucial Parameter
- Analyzing the Charging Current
- Reaching Full Charge: Asymptotic Behavior
- Practical Applications: Where RC Circuits Shine
- 1. Timing Circuits:
- 2. Filtering Circuits:
- 3. Pulse Shaping Circuits:
- 4. Energy Storage:
- 5. Camera Autofocus Systems:
- Designing RC Circuits: Choosing the Right Components
- Troubleshooting RC Circuits: Common Issues
- Beyond the Basics: Advanced Considerations
- Conclusion: Mastering the RC Circuit
- Latest Posts
- Latest Posts
- Related Post
Charging an Initially Uncharged Capacitor Through a Resistor: A Comprehensive Guide
Charging a capacitor through a resistor is a fundamental concept in electronics, crucial for understanding circuits involving timing, energy storage, and signal processing. This process is governed by simple yet powerful equations that describe the exponential growth of voltage across the capacitor. This in-depth guide will explore the theory, practical applications, and nuances of charging a capacitor through a resistor.
The RC Circuit: The Heart of the Matter
The core of capacitor charging involves an RC circuit, which consists of a resistor (R) and a capacitor (C) connected in series with a voltage source (often a battery). When the circuit is closed, current begins to flow, charging the capacitor. The resistor limits the rate of current flow, influencing the charging time.
Understanding the Components
-
Resistor (R): The resistor acts as a current-limiting element. Its resistance (measured in ohms) dictates how quickly the capacitor charges. A higher resistance leads to a slower charging time.
-
Capacitor (C): The capacitor stores electrical energy in an electric field between its plates. Its capacitance (measured in farads) determines its energy storage capacity. A larger capacitance means the capacitor can store more charge at a given voltage.
-
Voltage Source (V): This is the source of electrical potential that drives the charging process. This could be a battery, power supply, or another voltage source.
The Charging Process: An Exponential Rise
The voltage across the capacitor doesn't jump instantly to the source voltage. Instead, it increases exponentially over time. This exponential rise is described by the following equation:
V<sub>c</sub>(t) = V<sub>s</sub>(1 - e<sup>-t/RC</sup>)
Where:
- V<sub>c</sub>(t) is the voltage across the capacitor at time t.
- V<sub>s</sub> is the source voltage.
- R is the resistance in ohms.
- C is the capacitance in farads.
- e is the base of the natural logarithm (approximately 2.718).
- RC is the time constant, denoted by τ (tau).
The Time Constant (τ = RC): A Crucial Parameter
The time constant, τ (tau), represents the time it takes for the capacitor voltage to reach approximately 63.2% of the source voltage. It's a crucial parameter for characterizing the charging speed of the RC circuit. A larger time constant implies a slower charging process.
- Short Time Constant: A small R or C value results in a short time constant, meaning the capacitor charges quickly.
- Long Time Constant: A large R or C value results in a long time constant, indicating a slower charging process.
Analyzing the Charging Current
While the capacitor voltage rises exponentially, the charging current behaves differently. Initially, the current is at its maximum value, determined by Ohm's Law (I = V<sub>s</sub>/R). As the capacitor charges, the voltage across it increases, reducing the voltage difference across the resistor. Consequently, the current decreases exponentially, following this equation:
I(t) = (V<sub>s</sub>/R)e<sup>-t/RC</sup>
Reaching Full Charge: Asymptotic Behavior
Theoretically, the capacitor never fully charges to the source voltage. The exponential nature of the charging process means the voltage approaches V<sub>s</sub> asymptotically. However, practically speaking, after approximately 5 time constants (5τ), the capacitor is considered fully charged, reaching over 99% of the source voltage.
Practical Applications: Where RC Circuits Shine
RC circuits are ubiquitous in electronics, finding applications in various areas:
1. Timing Circuits:
-
Timers: RC circuits are fundamental to simple timers, like those used in blinking LEDs or controlling the timing of various events in microcontrollers. By carefully selecting the R and C values, you can precisely control the timing intervals.
-
Delay Circuits: Creating delays in circuits is essential in many applications. An RC circuit can provide a simple and effective way to introduce a controlled delay before an action occurs.
2. Filtering Circuits:
-
Low-Pass Filters: RC circuits act as low-pass filters, allowing low-frequency signals to pass through while attenuating high-frequency signals. This is crucial in noise reduction and signal conditioning.
-
High-Pass Filters: By changing the component arrangement, an RC circuit can function as a high-pass filter, allowing high-frequency signals to pass through and blocking low-frequency ones.
3. Pulse Shaping Circuits:
- Smoothing Pulses: RC circuits help smooth out irregular pulses, making them more predictable and easier to process. This is especially valuable in signal processing applications where clean signals are essential.
4. Energy Storage:
- Flash Photography: While more sophisticated systems exist today, flash photography once heavily relied on RC circuits to rapidly charge capacitors that provide the energy for the flash.
5. Camera Autofocus Systems:
- Focus Motor Control: Certain autofocus systems utilize RC circuits for controlling the speed and precision of the focus motor adjustments.
Designing RC Circuits: Choosing the Right Components
Designing an RC circuit involves selecting appropriate resistor and capacitor values to achieve the desired time constant and circuit behavior. The following factors are crucial considerations:
-
Desired Time Constant (τ): The desired charging time dictates the product of R and C.
-
Component Tolerances: Real-world resistors and capacitors have inherent tolerances, meaning their actual values may slightly deviate from their nominal values. This should be accounted for during circuit design to ensure proper operation within a specified range.
-
Power Dissipation: Resistors dissipate power during the charging process. The power dissipation (P = I²R) must be within the resistor's power rating to avoid overheating and damage.
-
Capacitor Voltage Rating: The capacitor must have a voltage rating that exceeds the source voltage to prevent breakdown.
Troubleshooting RC Circuits: Common Issues
While RC circuits are relatively simple, some common issues can arise:
-
Incorrect Component Values: Using incorrect R or C values leads to an incorrect time constant and potentially malfunctioning circuits.
-
Open or Short Circuits: Open circuits prevent current flow, while short circuits can cause excessive current and component damage.
-
Faulty Components: Defective resistors or capacitors may not perform as expected.
-
Improper Wiring: Incorrect wiring can also lead to circuit malfunction.
Beyond the Basics: Advanced Considerations
-
Nonlinear Resistors: While we often assume linear resistors, using nonlinear resistors (like thermistors) can introduce more complex charging behavior.
-
Multiple RC Circuits: Cascading RC circuits allows for more sophisticated timing control and filtering.
-
Op-Amps with RC Circuits: Combining RC circuits with operational amplifiers enables the creation of advanced circuits with more precise control over voltage and timing.
Conclusion: Mastering the RC Circuit
Understanding the charging of an initially uncharged capacitor through a resistor is paramount for anyone involved in electronics. This process, governed by the simple yet powerful exponential equation, forms the basis for numerous applications in various fields. By understanding the time constant, current behavior, and practical considerations, you can design and troubleshoot RC circuits effectively. This guide provides a solid foundation for further exploration into the fascinating world of electronics and the versatile capabilities of RC circuits. The comprehensive explanation of theory, applications, and troubleshooting techniques will equip you with the knowledge to confidently tackle projects involving capacitor charging. Remember to always consider the practical aspects of component selection and power dissipation for successful circuit implementation.
Latest Posts
Latest Posts
-
Determine The Magnitude Of The Pin Force At A
Mar 27, 2025
-
What Is The Advantage Of Using A Wet Mount
Mar 27, 2025
-
What Is The Name Of The Following
Mar 27, 2025
-
The Rate At Which Energy Is Used Is Called
Mar 27, 2025
-
Accepting A Special Order Will Improve
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about You Charge An Initially Uncharged Capacitor Through Resistor . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
