Written Assignment 7 Dilations And Symmetry
Holbox
Mar 28, 2025 · 6 min read
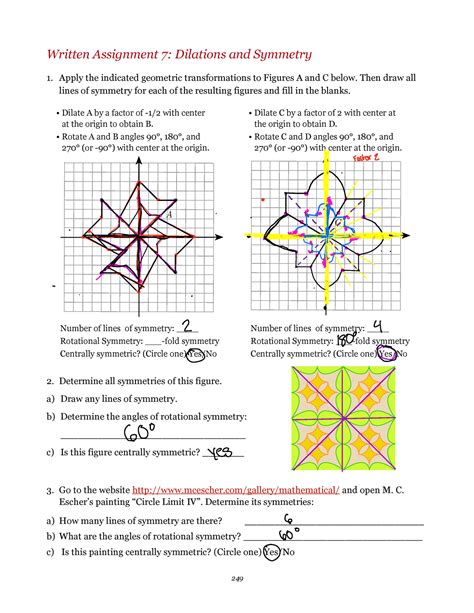
Table of Contents
- Written Assignment 7 Dilations And Symmetry
- Table of Contents
- Written Assignment 7: Dilations and Symmetry – A Comprehensive Guide
- Understanding Dilations
- Properties of Dilations
- Understanding Symmetry
- Relationship Between Dilations and Symmetry
- Solving Problems Involving Dilations and Symmetry
- Advanced Concepts and Applications
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Written Assignment 7: Dilations and Symmetry – A Comprehensive Guide
This comprehensive guide delves into the intricacies of dilations and symmetry, providing a robust understanding of these geometrical concepts crucial for various mathematical applications. We will explore different types of dilations, their properties, and the relationship between dilations and symmetry. This guide aims to equip you with the knowledge and skills necessary to excel in your written assignment.
Understanding Dilations
A dilation is a transformation that changes the size of a figure, but not its shape. It's a type of geometric transformation that alters the scale of an object. Imagine enlarging or shrinking a photograph – that's essentially a dilation. The key elements defining a dilation are:
-
Center of Dilation: This is a fixed point around which the dilation occurs. Think of it as the "pivot point" for the transformation.
-
Scale Factor: This number determines the size change. A scale factor greater than 1 enlarges the figure (an enlargement), while a scale factor between 0 and 1 shrinks it (a reduction). A scale factor of 1 results in no change. A negative scale factor introduces a reflection as well as a change in size.
Types of Dilations:
We can categorize dilations based on their scale factor:
-
Enlargement: The scale factor (k) is greater than 1 (k > 1). The image is larger than the pre-image.
-
Reduction: The scale factor (k) is between 0 and 1 (0 < k < 1). The image is smaller than the pre-image.
-
Isometry (Special Case): When the scale factor is 1 (k = 1), the dilation results in a congruent image; it is essentially a translation (a slide) or a rotation (a turn) if the center of dilation is not on the figure itself.
-
Negative Dilation: When the scale factor is negative (k < 0), the dilation involves a reflection across the center of dilation, in addition to a change in size.
Properties of Dilations
Dilations preserve certain properties of the original figure:
-
Shape: The shape of the figure remains unchanged after dilation. Angles remain congruent.
-
Parallelism: Parallel lines remain parallel after dilation.
-
Colinearity: Points that are collinear before dilation remain collinear afterwards.
-
Ratio of Distances: The ratio of distances between corresponding points remains constant and equal to the scale factor.
Understanding Symmetry
Symmetry is a fundamental concept in geometry and beyond. It describes the invariance of a figure under certain transformations. Several types of symmetry exist:
-
Line Symmetry (Reflectional Symmetry): A figure possesses line symmetry if it can be folded along a line (the line of symmetry) such that the two halves coincide. This line of symmetry divides the figure into two mirror images.
-
Rotational Symmetry: A figure exhibits rotational symmetry if it can be rotated about a central point (the center of rotation) by a certain angle less than 360 degrees and still appear unchanged. The angle of rotation is often described as the order of rotational symmetry. For example, a square has rotational symmetry of order 4 (90°, 180°, 270°, 360°).
-
Point Symmetry (Central Symmetry): A figure has point symmetry if it can be rotated 180° about a point (the center of symmetry) and look identical. This is a special case of rotational symmetry.
-
Translational Symmetry: A figure possesses translational symmetry if it can be translated (moved) in a certain direction by a specific distance and still appear unchanged. This is often seen in repeating patterns.
Relationship Between Dilations and Symmetry
While seemingly distinct, dilations and symmetry are interconnected:
-
Dilations and Line Symmetry: A dilation centered on a line of symmetry will preserve the line symmetry. The resulting image will also have the same line of symmetry.
-
Dilations and Rotational Symmetry: A dilation centered on the center of rotational symmetry preserves the rotational symmetry. The image will possess the same order of rotational symmetry as the original.
-
Dilations and Point Symmetry: Similar to rotational symmetry, a dilation centered on a point of symmetry preserves the point symmetry.
Solving Problems Involving Dilations and Symmetry
Let's explore some practical examples to solidify our understanding:
Example 1: Finding the Coordinates of Dilated Points
Consider a triangle with vertices A(1, 1), B(3, 1), and C(2, 4). Find the coordinates of the vertices of the dilated triangle with a scale factor of 2 and a center of dilation at the origin (0, 0).
Solution:
Multiply the coordinates of each vertex by the scale factor:
- A'(2 * 1, 2 * 1) = A'(2, 2)
- B'(2 * 3, 2 * 1) = B'(6, 2)
- C'(2 * 2, 2 * 4) = C'(4, 8)
The dilated triangle has vertices A'(2, 2), B'(6, 2), and C'(4, 8).
Example 2: Determining the Scale Factor
Two similar triangles are given. Triangle ABC has sides of length 4, 6, and 8. Triangle A'B'C' has sides of length 2, 3, and 4. Determine the scale factor of the dilation that maps triangle ABC to triangle A'B'C'.
Solution:
The scale factor is the ratio of the corresponding sides of the two similar triangles. Let's use the ratio of the longest sides:
Scale Factor = Length of A'C' / Length of AC = 4 / 8 = 1/2
The scale factor is 1/2, indicating a reduction.
Example 3: Identifying Symmetry after Dilation
A square with vertices (0,0), (1,0), (1,1), (0,1) undergoes a dilation with a scale factor of 3 and a center of dilation at (0,0). Does the dilated figure retain its symmetry?
Solution:
The dilated square will have vertices (0,0), (3,0), (3,3), (0,3). This is still a square, meaning it retains its four lines of symmetry, its rotational symmetry of order 4, and its point symmetry. The dilation, centered at the center of symmetry, preserves all symmetries.
Example 4: Combining Dilations and Reflections
A rectangle ABCD with vertices A(1,1), B(3,1), C(3,2), D(1,2) is dilated by a scale factor of -2 centered at the origin. Describe the resulting image.
Solution:
Each point's coordinates will be multiplied by -2. This will create a larger rectangle, but it will also reflect across the origin. The new vertices will be A'(-2, -2), B'(-6, -2), C'(-6,-4), D'(-2,-4). The resulting rectangle is larger than the original and is a reflection.
Advanced Concepts and Applications
The concepts of dilations and symmetry extend beyond basic geometry and find applications in various fields:
-
Computer Graphics: Dilations are fundamental to image scaling and resizing in computer graphics.
-
Fractals: Many fractals are constructed using iterative dilations and self-similarity.
-
Cartography: Map projections often involve dilations and scaling to represent the curved surface of the Earth on a flat plane.
-
Engineering and Design: Understanding symmetry and dilations is crucial in designing structures, creating symmetrical patterns, and scaling blueprints.
Conclusion
Understanding dilations and symmetry is paramount for a solid foundation in geometry and its applications. This guide has explored these concepts in detail, providing examples and explanations to help you master these essential mathematical tools. Remember that practice is key to proficiency; work through various problems, experimenting with different scale factors and centers of dilation, to build a strong understanding of these transformations and their interplay with various types of symmetry. By mastering these concepts, you will be well-prepared to tackle any written assignment or real-world problem involving dilations and symmetry. The combination of theoretical knowledge and practical application will ultimately lead to success in this area of mathematics. Remember to always clearly define your transformations, show your work meticulously, and accurately interpret the results. Good luck with your written assignment!
Latest Posts
Latest Posts
-
Strategic Intent Refers To A Situation Where A Company
Apr 01, 2025
-
Which Of These Events Occurred First
Apr 01, 2025
-
What Are Homemade Dividends And Why Would Investors Make Them
Apr 01, 2025
-
Which Of The Following Is A Normative Statement
Apr 01, 2025
-
Label The Midsagittal Male Pelvis Using The Hints Provided
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Written Assignment 7 Dilations And Symmetry . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
