Write An Equation For The Function Graphed Below
Holbox
Mar 31, 2025 · 6 min read
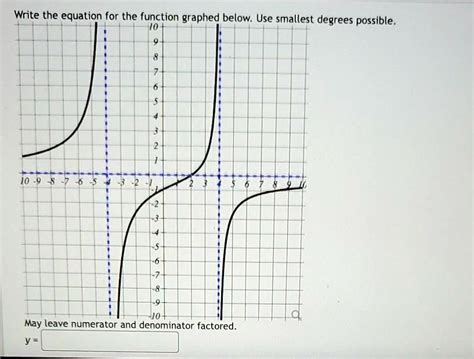
Table of Contents
- Write An Equation For The Function Graphed Below
- Table of Contents
- Write an Equation for the Function Graphed Below: A Comprehensive Guide
- Understanding the Basics: Key Features to Analyze
- 1. Intercepts: Where the Graph Meets the Axes
- 2. Asymptotes: Lines the Graph Approaches but Never Touches
- 3. Turning Points (Extrema): Local Maxima and Minima
- 4. Symmetry: Even, Odd, or Neither
- Different Function Types and Their Equations
- 1. Linear Functions (Straight Lines)
- 2. Quadratic Functions (Parabolas)
- 3. Polynomial Functions (Higher Degree)
- 4. Rational Functions
- 5. Exponential Functions
- 6. Trigonometric Functions
- 7. Logarithmic Functions
- Advanced Techniques and Considerations
- Importance of Context and Multiple Solutions
- Latest Posts
- Latest Posts
- Related Post
Write an Equation for the Function Graphed Below: A Comprehensive Guide
Determining the equation of a function from its graph is a fundamental skill in mathematics, particularly in algebra and calculus. This process involves analyzing key features of the graph such as intercepts, asymptotes, turning points, and overall behavior to deduce the underlying mathematical relationship. This article will guide you through various methods and strategies for writing the equation of a function given its graph, addressing different types of functions and complexities.
Understanding the Basics: Key Features to Analyze
Before we dive into specific examples, let's review some critical features of a graph that provide crucial clues for determining its equation:
1. Intercepts: Where the Graph Meets the Axes
- x-intercepts: The points where the graph intersects the x-axis. At these points, the y-coordinate is zero. X-intercepts represent the roots or zeros of the function.
- y-intercept: The point where the graph intersects the y-axis. At this point, the x-coordinate is zero. The y-intercept represents the value of the function when x=0.
2. Asymptotes: Lines the Graph Approaches but Never Touches
- Vertical Asymptotes: Vertical lines (x = c) that the graph approaches as x approaches a specific value (c). These often indicate division by zero in the function's equation.
- Horizontal Asymptotes: Horizontal lines (y = c) that the graph approaches as x approaches positive or negative infinity. These indicate the function's behavior as x becomes very large or very small.
- Oblique (Slant) Asymptotes: Diagonal lines that the graph approaches as x approaches positive or negative infinity. These are typically found in rational functions where the degree of the numerator is one greater than the degree of the denominator.
3. Turning Points (Extrema): Local Maxima and Minima
Turning points represent points where the function changes from increasing to decreasing or vice versa. These points can be helpful in determining the degree and general shape of the function. Identifying these points often requires calculus techniques.
4. Symmetry: Even, Odd, or Neither
- Even Functions: Symmetric about the y-axis. f(-x) = f(x) (e.g., parabolas)
- Odd Functions: Symmetric about the origin. f(-x) = -f(x) (e.g., cubic functions like y=x³)
- Neither: Functions that exhibit neither even nor odd symmetry.
Different Function Types and Their Equations
Let's explore how to determine the equation for various types of functions based on their graphical representation:
1. Linear Functions (Straight Lines)
Linear functions have the general form y = mx + b, where 'm' is the slope and 'b' is the y-intercept.
- Finding the Slope (m): Choose two points (x1, y1) and (x2, y2) on the line and use the formula: m = (y2 - y1) / (x2 - x1)
- Finding the y-intercept (b): This is the y-coordinate where the line crosses the y-axis. Alternatively, substitute one point and the slope into the equation y = mx + b and solve for b.
Example: A line passes through points (1, 2) and (3, 6). The slope is (6-2)/(3-1) = 2. Using the point (1,2), we get 2 = 2(1) + b, so b = 0. The equation is y = 2x.
2. Quadratic Functions (Parabolas)
Quadratic functions have the general form y = ax² + bx + c, where 'a', 'b', and 'c' are constants.
- Finding 'a', 'b', and 'c':
- Vertex Form: If the vertex (h, k) is visible, use the vertex form: y = a(x - h)² + k. Find 'a' by substituting another point on the parabola.
- Standard Form: If the x-intercepts (roots) are visible, use the factored form: y = a(x - r1)(x - r2), where r1 and r2 are the x-intercepts. Find 'a' by substituting another point.
- General Form: Use three points on the parabola to create a system of three equations with three unknowns ('a', 'b', 'c') and solve the system.
Example: A parabola passes through points (-1, 0), (1, 0), and (0, -1). The x-intercepts are -1 and 1, so the factored form is y = a(x + 1)(x - 1). Substituting (0, -1), we get -1 = a(1)(-1), so a = 1. The equation is y = x² - 1.
3. Polynomial Functions (Higher Degree)
Polynomial functions have the general form y = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀, where 'n' is the degree of the polynomial.
Determining the equation for higher-degree polynomials is more complex and often requires knowledge of the roots (x-intercepts) and their multiplicities (how many times the root appears). The more points you have, the easier it becomes to solve for the coefficients. Techniques like polynomial interpolation can be utilized.
4. Rational Functions
Rational functions are functions of the form y = P(x) / Q(x), where P(x) and Q(x) are polynomials.
- Identifying Vertical Asymptotes: These occur where Q(x) = 0.
- Identifying Horizontal Asymptotes: These depend on the degrees of P(x) and Q(x).
- Finding Intercepts: Substitute x = 0 for the y-intercept and solve P(x) = 0 for the x-intercepts.
Example: A rational function has vertical asymptotes at x = 2 and x = -2 and a horizontal asymptote at y = 1. A possible equation would be y = (x²)/(x² - 4). Note that multiple equations could fit this description. More points would be needed for a definitive equation.
5. Exponential Functions
Exponential functions have the general form y = abˣ, where 'a' is the initial value and 'b' is the base.
- Finding 'a' and 'b': Use two points (x1, y1) and (x2, y2) on the graph to create a system of two equations: y1 = abˣ¹ and y2 = abˣ². Solve this system for 'a' and 'b'.
Example: An exponential function passes through points (0, 2) and (1, 6). Substituting into the general form: 2 = ab⁰ and 6 = ab¹. This gives a = 2 and b = 3. The equation is y = 2(3ˣ).
6. Trigonometric Functions
Trigonometric functions involve sine, cosine, tangent, and their reciprocals. Determining the equation often involves identifying the amplitude, period, phase shift, and vertical shift.
7. Logarithmic Functions
Logarithmic functions are the inverse of exponential functions and have the general form y = logₐ(x), where 'a' is the base. The graph of a logarithmic function will have a vertical asymptote.
Advanced Techniques and Considerations
For more complex functions or when the graph doesn't provide enough clear information, more advanced techniques may be necessary:
- Curve Fitting: Using software or statistical methods to find the best-fitting curve to a set of data points.
- Calculus: Using derivatives to determine the function's rate of change and find critical points (maxima and minima).
- Numerical Methods: Approximating the function's equation using numerical techniques like interpolation.
Importance of Context and Multiple Solutions
It's crucial to remember that in some cases, multiple functions could potentially match a given graph. The accuracy of the determined equation depends heavily on the accuracy and detail of the graph. The context of the problem (e.g., application in physics, engineering) may also provide additional constraints or clues to help narrow down possibilities. Always carefully consider all the available information before writing down the equation.
By systematically analyzing the key features of a graph and applying the appropriate techniques for different function types, one can effectively determine the equation that represents the visual data. Practice and understanding of various function properties are essential for mastering this skill. Remember to always double-check your work and consider the limitations of graphical analysis.
Latest Posts
Latest Posts
-
What Pressure Is Required To Contain 0 023 Moles Of Nitrogen
Apr 03, 2025
-
The Steel Shaft Is Made From Two Segments
Apr 03, 2025
-
Which Of The Following Are True About Outgroups
Apr 03, 2025
-
A Joint Venture Establishes A New Business That Is
Apr 03, 2025
-
A Hazardous Material Spill Occurred During Transportation
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Write An Equation For The Function Graphed Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
