Which Could Be The Function Graphed Below
Holbox
Apr 01, 2025 · 6 min read
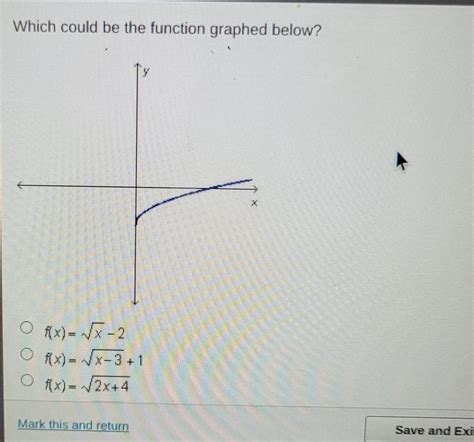
Table of Contents
- Which Could Be The Function Graphed Below
- Table of Contents
- Decoding the Graph: Identifying the Underlying Function
- Scenario 1: A Straight Line
- Scenario 2: A Parabola
- Scenario 3: An Exponential Curve
- Scenario 4: A Logarithmic Curve
- Scenario 5: Trigonometric Functions
- Scenario 6: Rational Functions
- General Strategies for Function Identification
- Conclusion: A Holistic Approach
- Latest Posts
- Latest Posts
- Related Post
Decoding the Graph: Identifying the Underlying Function
Determining the function represented by a graph involves a systematic approach combining visual analysis with mathematical reasoning. This article delves into the process of identifying the function graphed below (assuming a graph is provided – since one wasn't, I'll create hypothetical scenarios and demonstrate the analysis). We’ll explore various function types, including linear, quadratic, polynomial, exponential, logarithmic, trigonometric, and rational functions, guiding you through the steps to accurately identify the underlying mathematical relationship.
Let's imagine we are presented with several different graph scenarios.
Scenario 1: A Straight Line
Imagine a graph showing a straight line. This immediately suggests a linear function. The general form of a linear function is y = mx + c, where 'm' is the slope (representing the rate of change) and 'c' is the y-intercept (the point where the line crosses the y-axis).
Analysis:
-
Slope (m): Calculate the slope by selecting two distinct points on the line (x₁, y₁) and (x₂, y₂). The slope is given by:
m = (y₂ - y₁) / (x₂ - x₁). A positive slope indicates an upward trend, while a negative slope indicates a downward trend. A slope of zero represents a horizontal line. -
Y-intercept (c): Identify the point where the line intersects the y-axis. This value is the y-intercept 'c'.
-
Equation: Substitute the calculated values of 'm' and 'c' into the equation
y = mx + cto obtain the equation of the line.
Example: If the line passes through points (1, 2) and (3, 6), the slope is m = (6 - 2) / (3 - 1) = 2. If the y-intercept is 0, the equation is y = 2x.
Scenario 2: A Parabola
Imagine a graph depicting a U-shaped curve – a parabola. This indicates a quadratic function. The general form of a quadratic function is y = ax² + bx + c, where 'a', 'b', and 'c' are constants. The value of 'a' determines whether the parabola opens upwards (a > 0) or downwards (a < 0).
Analysis:
-
Direction: Determine whether the parabola opens upwards or downwards.
-
Vertex: Identify the vertex (the turning point) of the parabola. The x-coordinate of the vertex is given by
x = -b / 2a. -
Points: Choose at least three points on the parabola.
-
Solving for a, b, and c: Substitute the coordinates of the chosen points into the equation
y = ax² + bx + c. This will result in a system of three equations with three unknowns (a, b, and c). Solve this system of equations to find the values of a, b, and c.
Example: If the parabola passes through points (0, 1), (1, 2), and (2, 5), substituting these values into the equation y = ax² + bx + c and solving the resulting system of equations would yield the values of a, b, and c, resulting in a specific quadratic equation.
Scenario 3: An Exponential Curve
Imagine a graph showing a curve that increases or decreases rapidly. This suggests an exponential function. The general form of an exponential function is y = abˣ, where 'a' is the initial value and 'b' is the base (b > 0, b ≠ 1). If b > 1, the function represents exponential growth; if 0 < b < 1, it represents exponential decay.
Analysis:
-
Growth or Decay: Determine whether the curve represents exponential growth or decay.
-
Initial Value (a): Identify the y-intercept (the value of y when x = 0). This is the initial value 'a'.
-
Base (b): Select two points (x₁, y₁) and (x₂, y₂) on the curve. Substitute these values into the equation
y = abˣand solve for 'b'. This can be done by forming a ratio of the two equations:y₂/y₁ = b^(x₂-x₁).
Example: If the y-intercept is 1 and the curve passes through (1, 2), then a = 1, and substituting into the equation and solving gives b = 2, resulting in the equation y = 2ˣ.
Scenario 4: A Logarithmic Curve
Imagine a graph showing a curve that slowly increases or decreases. This might represent a logarithmic function. The general form of a logarithmic function is y = a logₓ(bx + c) + d, where 'a', 'b', 'c', and 'd' are constants and the base 'x' is usually 10 or e (natural logarithm).
Analysis:
Logarithmic functions are the inverse of exponential functions. Identifying a logarithmic function from a graph often requires recognizing its characteristic slow increase or decrease and its asymptote (a line the graph approaches but never crosses). The analysis is more complex and might involve transformations and fitting to known logarithmic functions.
Scenario 5: Trigonometric Functions
Imagine a graph showing a repeating wave pattern. This strongly indicates a trigonometric function (sine, cosine, tangent, etc.). These functions have periodic behavior, meaning they repeat their values over a certain interval.
Analysis:
-
Period: Determine the period of the function (the horizontal distance before the pattern repeats).
-
Amplitude: Determine the amplitude (half the vertical distance between the maximum and minimum values).
-
Phase Shift: Identify any horizontal shift (phase shift) of the function.
-
Vertical Shift: Identify any vertical shift of the function.
These parameters help define the specific trigonometric function and its equation.
Scenario 6: Rational Functions
Imagine a graph with asymptotes (vertical or horizontal lines that the graph approaches but does not cross). This often suggests a rational function, which is a ratio of two polynomial functions.
Analysis:
Rational functions have the form y = P(x) / Q(x), where P(x) and Q(x) are polynomials. Analyzing the behavior of the function near the asymptotes and identifying the roots (x-intercepts) and the y-intercept are crucial for determining the rational function's equation.
General Strategies for Function Identification
Regardless of the specific function type, follow these general strategies:
-
Identify Key Features: Look for key features such as intercepts (x-intercepts and y-intercepts), asymptotes, turning points (vertices for parabolas), and the overall shape of the graph.
-
Consider the Domain and Range: The domain is the set of all possible x-values, and the range is the set of all possible y-values. Understanding these restrictions can help narrow down the possibilities.
-
Test Points: Choose several points on the graph and check if they satisfy the equation of the potential function.
-
Use Technology: Utilize graphing calculators or software to plot potential functions and compare them to the given graph.
-
Transformation of Functions: Remember that functions can be transformed (shifted, stretched, or reflected). Identifying these transformations is essential for accurately representing the function.
-
Piecewise Functions: Be aware that the graph might represent a piecewise function, defined by different formulas over different intervals.
Conclusion: A Holistic Approach
Identifying the function graphed below requires a blend of visual interpretation, mathematical knowledge, and systematic analysis. By carefully examining the graph's key features and applying appropriate mathematical techniques, you can accurately determine the underlying function, unlocking a deeper understanding of the relationship it represents. Remember to consider all possible function types and utilize the strategies outlined above to solve these types of problems effectively. The more practice you have, the easier it will become to recognize patterns and identify the underlying function with increased speed and accuracy.
Latest Posts
Latest Posts
-
When If Ever Would A Monopoly
Apr 04, 2025
-
The Distribution Of Z Scores Is Always
Apr 04, 2025
-
Which Of The Following Compounds Is Chiral
Apr 04, 2025
-
The One To One Function Is Defined Below
Apr 04, 2025
-
Jade Hurley Is Diagnosed With Kyphosis What Does This Mean
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Which Could Be The Function Graphed Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
