Two Disks Are Rotating About The Same Axis
Holbox
Mar 30, 2025 · 6 min read
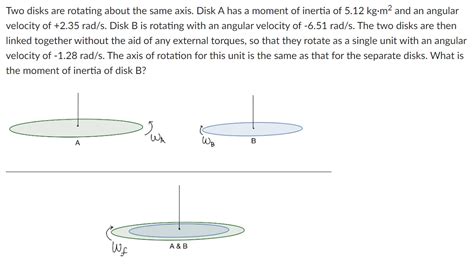
Table of Contents
- Two Disks Are Rotating About The Same Axis
- Table of Contents
- Two Disks Rotating About the Same Axis: A Deep Dive into Angular Momentum and Coupled Systems
- Angular Momentum: The Foundation of Rotational Motion
- Understanding Moment of Inertia
- Two Independent Disks: A Simple Case
- Coupled Disks: Introducing Interaction
- Conservation of Angular Momentum in Coupled Systems
- Real-World Applications: From Wind Turbines to Gyroscopes
- Advanced Considerations: Friction and Energy Loss
- Complex Couplings and Non-Linear Dynamics
- Further Exploration: Precession and Nutation
- Conclusion: A Dynamic System with Broad Implications
- Latest Posts
- Latest Posts
- Related Post
Two Disks Rotating About the Same Axis: A Deep Dive into Angular Momentum and Coupled Systems
Understanding the dynamics of rotating systems is crucial in various fields, from engineering and physics to astrophysics and even biology. This article delves deep into the fascinating mechanics of two disks rotating about the same axis, exploring concepts like angular momentum, conservation laws, and the complexities introduced by coupling. We'll examine both idealized scenarios and real-world applications, providing a comprehensive understanding of this fundamental physical system.
Angular Momentum: The Foundation of Rotational Motion
Before we analyze the behavior of two disks, let's solidify our understanding of angular momentum. Angular momentum (L) is the rotational equivalent of linear momentum. It's a vector quantity, meaning it possesses both magnitude and direction. The direction is determined by the right-hand rule: if you curl your fingers in the direction of rotation, your thumb points in the direction of the angular momentum vector.
The magnitude of angular momentum is given by:
L = Iω
Where:
-
I represents the moment of inertia, a measure of an object's resistance to changes in its rotational motion. It depends on the object's mass distribution and its axis of rotation. A disk's moment of inertia about its central axis is (1/2)MR², where M is the mass and R is the radius.
-
ω represents the angular velocity, the rate of change of angular displacement.
Understanding Moment of Inertia
The moment of inertia is a critical parameter in understanding rotational dynamics. It's not simply the mass; it also considers how that mass is distributed relative to the axis of rotation. A disk with most of its mass concentrated near the rim will have a larger moment of inertia than a disk with the same mass but with mass distributed more evenly. This means the second disk will require more torque to change its angular velocity. This concept is vital when considering the interaction of two rotating disks.
Two Independent Disks: A Simple Case
Let's start with the simplest scenario: two disks rotating independently about the same axis, with no interaction between them. Each disk possesses its own angular momentum, and the total angular momentum of the system is simply the vector sum of the individual angular momenta. If both disks rotate in the same direction, the total angular momentum is the sum of their individual angular momenta. If they rotate in opposite directions, the total angular momentum is the difference. Crucially, in the absence of external torques (twisting forces), the total angular momentum of this system remains constant – this is the principle of conservation of angular momentum.
Coupled Disks: Introducing Interaction
The situation becomes far more interesting when the two disks are coupled, meaning they can interact and exchange energy. This interaction might occur through various mechanisms:
-
Mechanical Coupling: A direct physical connection, such as a shaft or gears, transfers torque between the disks. This is common in many mechanical systems.
-
Magnetic Coupling: Magnetic fields can induce torques on the disks, especially if they have conducting material.
-
Fluid Coupling: A fluid medium connecting the disks can transfer energy through viscous forces.
The type of coupling dramatically affects the dynamics of the system. With mechanical coupling, a faster-rotating disk will tend to accelerate the slower one, while simultaneously slowing down itself. This transfer of angular momentum continues until both disks reach a common angular velocity, provided there's no external torque. The final angular velocity depends on the initial angular momenta and the moments of inertia of both disks.
Conservation of Angular Momentum in Coupled Systems
Even with coupling, the principle of conservation of angular momentum holds true as long as there are no external torques. The total angular momentum of the system before coupling is equal to the total angular momentum after coupling. This means we can predict the final angular velocity of the coupled system based on the initial conditions:
L_initial = L_final
Where L_initial is the sum of the angular momenta of the two disks before coupling, and L_final is the angular momentum of the coupled system after they reach a common angular velocity. This allows for calculation of the final angular velocity (ω_final) using the combined moment of inertia (I_total):
I₁ω₁ + I₂ω₂ = (I₁ + I₂)ω_final
This equation highlights the importance of both the individual moments of inertia and the initial angular velocities in determining the final state of the system.
Real-World Applications: From Wind Turbines to Gyroscopes
The principles governing two rotating disks find widespread application in various real-world scenarios:
-
Wind Turbines: The gearbox in a wind turbine efficiently transfers the rotational energy from the slowly rotating blades to a faster-rotating generator. This involves carefully designed couplings between different rotating components.
-
Automotive Transmissions: Gear systems in cars involve multiple coupled rotating disks (gears) that allow for efficient power transmission at different speeds.
-
Gyroscopes: Gyroscopes utilize the conservation of angular momentum to maintain stability and orientation. The spinning rotor is a prime example of a rotating disk, and its stability arises from the resistance to changes in its angular momentum.
Advanced Considerations: Friction and Energy Loss
Our analysis so far has assumed ideal conditions with no energy loss. However, in real-world systems, friction plays a significant role. Frictional forces between the disks, the bearings, and the surrounding environment dissipate energy as heat, leading to a decrease in the total kinetic energy of the system. This energy loss means that the final angular velocity of the coupled system will be lower than predicted by the ideal conservation of angular momentum equation. Accurate modeling of these systems requires considering frictional losses and potentially more sophisticated mathematical techniques.
Complex Couplings and Non-Linear Dynamics
In more complex scenarios, the coupling between the disks might not be constant or linear. For example, the torque transmitted between the disks might depend on their relative angular velocities in a non-linear fashion. This introduces greater complexities into the analysis, often requiring numerical methods or advanced mathematical tools to solve. These systems can exhibit chaotic behavior under certain conditions, making their prediction challenging.
Further Exploration: Precession and Nutation
When we move beyond simple axial rotation, other fascinating phenomena emerge. If the axis of rotation of a spinning disk is not fixed, it can experience precession – a slow, conical rotation of the axis itself. This phenomenon is closely related to angular momentum and is crucial to understanding the behavior of gyroscopes and tops. Additionally, nutation, an oscillation of the axis of rotation superimposed on precession, can occur in real-world systems.
Conclusion: A Dynamic System with Broad Implications
The seemingly simple system of two disks rotating about the same axis reveals a rich tapestry of physical principles, from fundamental conservation laws to complex non-linear dynamics. Understanding this system is crucial in various fields, providing valuable insights into the behavior of rotating machinery, gyroscopic systems, and numerous other engineering and scientific applications. Further exploration into the intricacies of coupling, frictional losses, and advanced phenomena like precession and nutation will continue to expand our understanding of this dynamic and significant physical system. The principles discussed here serve as a foundational stepping stone for delving into more intricate rotational dynamics.
Latest Posts
Latest Posts
-
You Can Recognize The Process Of Pinocytosis When
Apr 01, 2025
-
Draw The Correct Product For The Given Diels Alder Reaction
Apr 01, 2025
-
Match Each Example Below To The Correct Cost Type
Apr 01, 2025
-
Developing Person Through Childhood And Adolescence
Apr 01, 2025
-
The Following Picture Would Be Best Described As
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Two Disks Are Rotating About The Same Axis . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
