Two Blocks Are Connected By A String
Holbox
Mar 24, 2025 · 7 min read
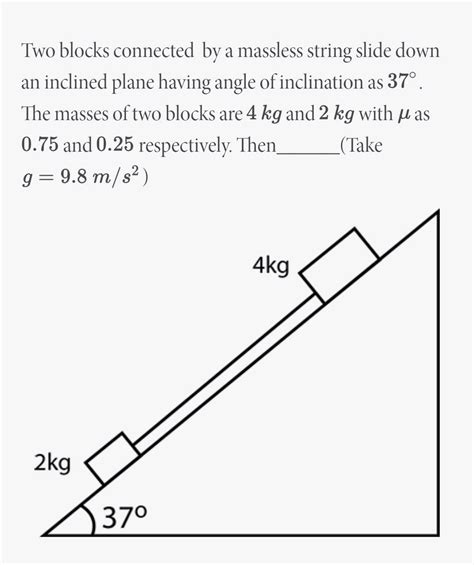
Table of Contents
- Two Blocks Are Connected By A String
- Table of Contents
- Two Blocks Connected by a String: Exploring the Physics of Coupled Systems
- Understanding the Basic Setup
- Key Concepts to Grasp
- Scenario 1: Two Blocks on a Frictionless Horizontal Surface
- Scenario 2: Introducing Friction
- Scenario 3: Inclined Plane
- Scenario 4: Introducing a Pulley
- Pulley System Analysis:
- Solving Problems Involving Two Blocks Connected by a String
- Advanced Considerations:
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Two Blocks Connected by a String: Exploring the Physics of Coupled Systems
The seemingly simple scenario of two blocks connected by a string opens a fascinating window into the world of physics, specifically mechanics. This seemingly basic setup allows us to explore fundamental concepts like Newton's Laws of Motion, forces, tension, friction, and the behavior of coupled systems. This article delves deep into the mechanics of this system, examining different scenarios, including frictionless surfaces, inclined planes, and the introduction of pulleys. We'll also look at how to solve problems involving these systems, providing a comprehensive guide for students and enthusiasts alike.
Understanding the Basic Setup
Imagine two blocks, let's call them block A and block B, connected by an inextensible string. This means the string's length remains constant throughout the system's motion. The blocks can rest on a surface (which may or may not be frictionless), and an external force might be applied to one of them. The string transmits tension throughout the system.
Key Concepts to Grasp
Before we dive into specific scenarios, it's essential to understand the following concepts:
- Newton's Laws of Motion: These are the bedrock of classical mechanics. They dictate how objects respond to forces. We'll primarily use Newton's Second Law (F=ma) to analyze the motion of the blocks.
- Tension: The force transmitted through the string. Tension acts equally and oppositely at both ends of the string. A taut string implies a non-zero tension force.
- Friction: The force that opposes motion between surfaces in contact. Friction depends on the nature of the surfaces and the normal force pressing them together. We'll often consider both static friction (preventing motion) and kinetic friction (opposing motion).
- Free-Body Diagrams: These diagrams visually represent all the forces acting on an object. Creating accurate free-body diagrams is crucial for correctly applying Newton's Laws.
- Mass and Acceleration: The mass of the blocks determines their inertia (resistance to changes in motion), and acceleration represents the rate of change of velocity.
Scenario 1: Two Blocks on a Frictionless Horizontal Surface
Let's begin with the simplest scenario: two blocks on a frictionless horizontal surface connected by a string. A horizontal force, F, is applied to block A.
Free-Body Diagrams:
- Block A: The forces acting on block A are the applied force F to the right, the tension T in the string to the left, and the normal force N<sub>A</sub> (equal and opposite to the weight of block A) from the surface.
- Block B: The forces acting on block B are the tension T to the right and the normal force N<sub>B</sub> (equal and opposite to the weight of block B) from the surface.
Equations of Motion:
Since the surface is frictionless, the only horizontal forces are the applied force and tension. Using Newton's Second Law:
- Block A: F - T = m<sub>A</sub>a (where m<sub>A</sub> is the mass of block A and 'a' is the acceleration of the system)
- Block B: T = m<sub>B</sub>a (where m<sub>B</sub> is the mass of block B)
By solving these two equations simultaneously, we can determine the acceleration 'a' and the tension T in the string.
Solution:
Substitute the second equation into the first: F - m<sub>B</sub>a = m<sub>A</sub>a. Solving for 'a', we get:
a = F / (m<sub>A</sub> + m<sub>B</sub>)
Then, substitute this value of 'a' back into the equation for block B to find the tension:
T = m<sub>B</sub>F / (m<sub>A</sub> + m<sub>B</sub>)
Scenario 2: Introducing Friction
Now let's introduce friction to the horizontal surface. We'll assume a coefficient of kinetic friction μ<sub>k</sub> between the blocks and the surface.
Free-Body Diagrams: The free-body diagrams remain similar, but we now include kinetic friction forces (f<sub>kA</sub> and f<sub>kB</sub>) opposing the motion of each block. These frictional forces are given by:
- f<sub>kA</sub> = μ<sub>k</sub>N<sub>A</sub> = μ<sub>k</sub>m<sub>A</sub>g
- f<sub>kB</sub> = μ<sub>k</sub>N<sub>B</sub> = μ<sub>k</sub>m<sub>B</sub>g (where 'g' is the acceleration due to gravity)
Equations of Motion:
- Block A: F - T - f<sub>kA</sub> = m<sub>A</sub>a
- Block B: T - f<sub>kB</sub> = m<sub>B</sub>a
Solving these equations simultaneously is more complex but follows the same principles as the frictionless case. The acceleration will be smaller due to the opposing frictional forces.
Scenario 3: Inclined Plane
Consider a more complex scenario: both blocks are on an inclined plane with an angle θ. Block A is positioned higher up the incline than block B.
Free-Body Diagrams: The forces acting on each block now include components of their weight parallel and perpendicular to the inclined plane.
Equations of Motion: The equations will incorporate the components of the weight parallel to the incline (m<sub>A</sub>g sinθ and m<sub>B</sub>g sinθ) and the frictional forces (if applicable). The normal forces will also change, as they are now perpendicular to the inclined plane.
Scenario 4: Introducing a Pulley
Adding a pulley significantly alters the system's dynamics. The pulley changes the direction of the tension force, allowing the blocks to move vertically or at different angles. We must also consider the possibility of pulley mass and friction in the pulley's axle.
Pulley System Analysis:
Analyzing a pulley system requires careful consideration of the forces and their directions. The tension in the string remains consistent throughout (assuming a massless, frictionless pulley). However, if the pulley has mass or friction, these factors must be included in the equations of motion. This introduces more complex calculations, but the core principle of applying Newton's Second Law to each block remains the same.
Solving Problems Involving Two Blocks Connected by a String
The key to solving these types of problems is a systematic approach:
- Draw Free-Body Diagrams: This is the most crucial step. Accurately depicting all forces acting on each block ensures that you account for every influence.
- Choose a Coordinate System: Select a coordinate system that simplifies the problem. This often involves aligning axes parallel and perpendicular to the direction of motion.
- Apply Newton's Second Law: Write down Newton's Second Law (F=ma) for each block in each direction. Resolve any forces into components along your chosen axes.
- Solve the Equations Simultaneously: The equations you've derived will usually be a system of simultaneous equations. Solve them algebraically to find the unknowns (acceleration and tension).
- Check your Solution: Ensure that the signs of your solutions make physical sense (e.g., acceleration should be positive in the direction you assumed).
Advanced Considerations:
- Non-ideal strings: Real-world strings have mass and may stretch slightly under tension. These factors can introduce additional complexities to the analysis.
- Inelastic collisions: If the blocks collide, momentum conservation principles must be applied.
- Energy considerations: Analyzing the system's energy (kinetic and potential) can provide another way to solve certain problems.
Conclusion
The seemingly simple system of two blocks connected by a string provides a rich learning environment for understanding fundamental physics principles. By systematically applying free-body diagrams, Newton's Laws, and careful consideration of forces and their interactions, you can solve a variety of problems related to coupled systems. This analysis lays a foundation for understanding more advanced topics in mechanics, including rotational motion, energy conservation, and the behavior of more complex systems. Understanding these core concepts opens doors to more advanced studies in physics and engineering. Mastering this topic helps build a strong foundation for further exploration of mechanics and related fields. The versatility of this system allows for numerous variations and complexities, providing continuous opportunities for problem-solving and deeper understanding. Continuous practice and exploration will enhance your analytical skills and deepen your understanding of classical mechanics.
Latest Posts
Latest Posts
-
The Center Of All Marketing Efforts Is
Mar 27, 2025
-
Methods To Minimize Agency Problem Include All Except
Mar 27, 2025
-
Which Command Mounts All Existing Filesystems In Etc Fstab
Mar 27, 2025
-
A Governments Policy Of Redistributing Income Makes The Income Distribution
Mar 27, 2025
-
Find A Formula For F Where It Is Defined
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Two Blocks Are Connected By A String . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
