Solve For Simplify Your Answer As Much As Possible
Holbox
Mar 26, 2025 · 5 min read
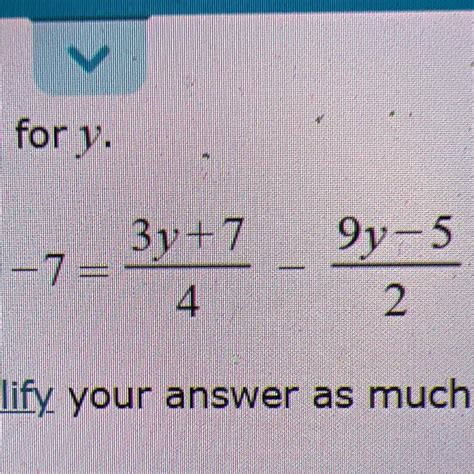
Table of Contents
- Solve For Simplify Your Answer As Much As Possible
- Table of Contents
- Solve and Simplify: A Comprehensive Guide to Mastering Algebraic Simplification
- Understanding the Basics: Like Terms and the Order of Operations
- Like Terms: The Foundation of Simplification
- PEMDAS/BODMAS: The Order of Operations
- Solving and Simplifying: A Step-by-Step Approach
- Advanced Simplification Techniques
- Factoring
- Rationalizing Denominators
- Simplifying Fractions
- Solving Equations: Applying Simplification
- Conclusion: Mastering Simplification for Mathematical Success
- Latest Posts
- Latest Posts
- Related Post
Solve and Simplify: A Comprehensive Guide to Mastering Algebraic Simplification
Simplifying algebraic expressions is a fundamental skill in mathematics, crucial for progressing through higher-level math concepts and problem-solving. While the core idea is straightforward—reduce an expression to its most concise and manageable form—the process can become complex depending on the expression's structure and the operations involved. This guide delves into various techniques to solve and simplify algebraic expressions, providing clear explanations and illustrative examples. We’ll explore different approaches, from combining like terms to applying the order of operations (PEMDAS/BODMAS) effectively and handling more advanced scenarios such as factoring and rationalizing denominators.
Understanding the Basics: Like Terms and the Order of Operations
Before tackling complex simplifications, let's solidify our understanding of the fundamental principles:
Like Terms: The Foundation of Simplification
Like terms are terms in an algebraic expression that have the same variables raised to the same powers. Only like terms can be combined. For example:
- 3x and -2x are like terms (both have 'x' raised to the power of 1).
- 5y² and y² are like terms (both have 'y' raised to the power of 2).
- 4ab and -7ab are like terms (both have 'a' and 'b' raised to the power of 1).
- 2x² and 3x are unlike terms (different powers of 'x').
Combining like terms involves adding or subtracting their coefficients (the numbers in front of the variables). For example:
3x + (-2x) = x (or 1x)
5y² + y² = 6y² (since the coefficient of y² is understood to be 1)
PEMDAS/BODMAS: The Order of Operations
The order of operations, represented by PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), dictates the sequence in which operations should be performed. Following this order is crucial for accurate simplification. Let's break it down:
-
Parentheses/Brackets: Solve any expressions within parentheses or brackets first. This often involves applying PEMDAS/BODMAS recursively within the parentheses.
-
Exponents/Orders: Evaluate any exponents (powers) or roots.
-
Multiplication and Division: Perform multiplication and division from left to right.
-
Addition and Subtraction: Perform addition and subtraction from left to right.
Solving and Simplifying: A Step-by-Step Approach
Let's now tackle more complex examples, demonstrating a systematic approach to solving and simplifying algebraic expressions.
Example 1: Combining Like Terms
Simplify: 3x² + 5x - 2x² + 7x - 4
Solution:
-
Identify like terms:
3x²and-2x²;5xand7x. -
Combine like terms:
3x² - 2x² = x²and5x + 7x = 12x. -
Rewrite the simplified expression:
x² + 12x - 4
Example 2: Applying PEMDAS/BODMAS
Simplify: 2(3x + 4) - 5x + 10
Solution:
-
Parentheses: Distribute the 2 across the terms inside the parentheses:
2 * 3x + 2 * 4 = 6x + 8. -
Rewrite the expression:
6x + 8 - 5x + 10 -
Combine like terms:
6x - 5x = xand8 + 10 = 18. -
Simplified expression:
x + 18
Example 3: Combining Like Terms and PEMDAS/BODMAS
Simplify: 3(x² - 2x + 1) + 2x(x - 3) - 5
Solution:
-
Parentheses: Distribute the 3 and 2x:
3x² - 6x + 3and2x² - 6x. -
Rewrite the expression:
3x² - 6x + 3 + 2x² - 6x - 5 -
Combine like terms:
3x² + 2x² = 5x²;-6x - 6x = -12x;3 - 5 = -2. -
Simplified expression:
5x² - 12x - 2
Advanced Simplification Techniques
As expressions become more intricate, we need to leverage more advanced techniques:
Factoring
Factoring involves expressing an expression as a product of simpler expressions. This is particularly useful for simplifying fractions and solving equations. Common factoring techniques include:
-
Greatest Common Factor (GCF): Find the largest factor common to all terms and factor it out. For example:
4x² + 8x = 4x(x + 2). -
Difference of Squares: Factor expressions of the form
a² - b²as(a + b)(a - b). For example:x² - 9 = (x + 3)(x - 3). -
Trinomial Factoring: Factor expressions of the form
ax² + bx + c. This often involves finding two numbers that add up to 'b' and multiply to 'ac'.
Rationalizing Denominators
Rationalizing a denominator involves eliminating radicals (square roots, cube roots, etc.) from the denominator of a fraction. This is done by multiplying both the numerator and the denominator by a suitable expression that eliminates the radical. For example:
To rationalize 1/√2, multiply both numerator and denominator by √2: 1/√2 * √2/√2 = √2/2
Simplifying Fractions
Simplifying fractions involves finding common factors in the numerator and denominator and canceling them out. This often requires factoring both the numerator and the denominator first. For example:
(x² - 4) / (x + 2) = [(x + 2)(x - 2)] / (x + 2) = x - 2 (assuming x ≠ -2)
Solving Equations: Applying Simplification
Simplification is crucial when solving equations. By simplifying both sides of an equation, you can make it easier to isolate the variable and find the solution.
Example:
Solve for x: 2(x + 3) = 4x - 2
Solution:
-
Simplify the left side:
2x + 6 -
Rewrite the equation:
2x + 6 = 4x - 2 -
Subtract 2x from both sides:
6 = 2x - 2 -
Add 2 to both sides:
8 = 2x -
Divide both sides by 2:
x = 4
Conclusion: Mastering Simplification for Mathematical Success
Mastering the art of solving and simplifying algebraic expressions is a cornerstone of mathematical proficiency. From combining like terms and applying the order of operations to employing advanced techniques like factoring and rationalizing denominators, the methods outlined in this guide provide a robust framework for simplifying a wide range of expressions. Remember, consistent practice and a systematic approach are key to building confidence and achieving fluency in algebraic simplification. The more you practice, the more readily you will recognize patterns and apply the most efficient techniques, paving the way for success in higher-level mathematics and problem-solving endeavors. By understanding and applying these concepts, you'll not only improve your accuracy but also develop a deeper understanding of mathematical relationships and their elegant expressions.
Latest Posts
Latest Posts
-
Photosystem I And Photosystem Ii Are Respectively Part Of
Mar 29, 2025
-
Why Is Social Media So Attractive To Consumers
Mar 29, 2025
-
The Industry Low Industry Average And Industry High Cost Benchmarks
Mar 29, 2025
-
The Categories Of Managerial Morality Include
Mar 29, 2025
-
How Is Stress Different From Force
Mar 29, 2025
Related Post
Thank you for visiting our website which covers about Solve For Simplify Your Answer As Much As Possible . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
