Find A Matrix A Such That
Holbox
Mar 30, 2025 · 5 min read
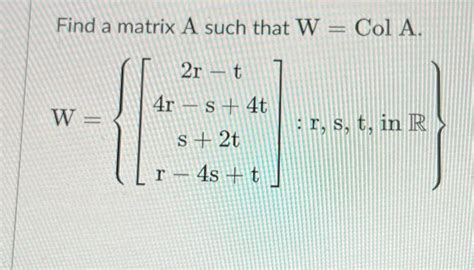
Table of Contents
- Find A Matrix A Such That
- Table of Contents
- Find a Matrix A Such That... A Comprehensive Guide
- Understanding the Problem
- Case 1: A Satisfies a Specific Equation
- Case 2: A Satisfies a Matrix Equation
- Case 3: A Satisfies a Condition on its Eigenvalues or Eigenvectors
- Case 4: A is Symmetric or Hermitian
- Case 5: A Satisfies a Rank Condition
- Advanced Techniques and Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Find a Matrix A Such That... A Comprehensive Guide
Finding a matrix A that satisfies a given condition is a fundamental problem in linear algebra. The specific condition dictates the approach, ranging from simple algebraic manipulation to more advanced techniques involving eigenvalues, eigenvectors, and matrix decompositions. This article explores various scenarios, providing detailed examples and explanations to guide you through the process. We'll cover several common "such that" conditions and demonstrate how to solve for matrix A effectively.
Understanding the Problem
The core of the problem "Find a matrix A such that..." lies in translating the "such that" clause into a system of equations or inequalities involving the elements of matrix A. This system can then be solved using standard linear algebra methods. The complexity depends heavily on the nature of the condition. Let's explore some examples.
Case 1: A Satisfies a Specific Equation
This is the most straightforward case. The condition might involve a specific equation relating A to another matrix or vector.
Example: Find a 2x2 matrix A such that A * [1; 2] = [3; 6].
Let A be represented as:
A = [[a, b],
[c, d]]
The equation becomes:
[[a, b],
[c, d]] * [1; 2] = [3; 6]
This leads to the following system of equations:
a + 2b = 3c + 2d = 6
This system has infinitely many solutions. We can express a = 3 - 2b and c = 6 - 2d. Therefore, there's a family of matrices A that satisfy the condition, each defined by choosing values for b and d. For instance, if b = 0 and d = 0, then A = [[3, 0], [6, 0]]. If b = 1 and d = 1, then A = [[1, 1], [4, 1]].
Case 2: A Satisfies a Matrix Equation
The condition may involve a matrix equation, often involving matrix multiplication, addition, or inversion.
Example: Find a 2x2 matrix A such that A * B = C, where B = [[1, 2], [3, 4]] and C = [[7, 10], [19, 26]].
Again, let A = [[a, b], [c, d]]. The equation A * B = C gives us:
[[a, b],
[c, d]] * [[1, 2],
[3, 4]] = [[7, 10],
[19, 26]]
This results in the following system:
a + 3b = 72a + 4b = 10c + 3d = 192c + 4d = 26
Solving this system (notice the second equation is a multiple of the first, and similarly for the third and fourth), we find a unique solution: a = 1, b = 2, c = 5, d = 4. Therefore, A = [[1, 2], [5, 4]].
Case 3: A Satisfies a Condition on its Eigenvalues or Eigenvectors
This is a more advanced scenario requiring knowledge of eigenvalues and eigenvectors. The condition may specify desired eigenvalues or eigenvectors for matrix A.
Example: Find a 2x2 matrix A such that it has eigenvalues λ₁ = 2 and λ₂ = 3, and corresponding eigenvectors v₁ = [1; 1] and v₂ = [1; -1].
We can construct matrix A using the eigenvectors and eigenvalues. Let P be the matrix whose columns are the eigenvectors, and D be the diagonal matrix with eigenvalues on the diagonal:
P = [[1, 1],
[1, -1]]
D = [[2, 0],
[0, 3]]
Then, matrix A can be found using the relationship A = PDP⁻¹:
First, find the inverse of P: P⁻¹ = [[-1/2, -1/2], [-1/2, 1/2]]
Then, calculate A:
A = [[1, 1],
[1, -1]] * [[2, 0],
[0, 3]] * [[-1/2, -1/2],
[-1/2, 1/2]] = [[5/2, -1/2], [-1/2, 5/2]]
Therefore, A = [[2.5, -0.5], [-0.5, 2.5]].
Case 4: A is Symmetric or Hermitian
If the condition specifies that A must be symmetric (A = Aᵀ) or Hermitian (A = Aᴴ), the problem simplifies due to the inherent constraints on the matrix elements.
Example: Find a symmetric 2x2 matrix A such that its trace is 5 and its determinant is 6.
Let A = [[a, b], [b, c]]. The trace is a + c = 5, and the determinant is ac - b² = 6. We have a system of two equations with three unknowns. We can express c = 5 - a and substitute into the second equation:
a(5 - a) - b² = 6 which simplifies to 5a - a² - b² = 6 or a² - 5a + b² = -6. This equation represents a family of solutions, each defined by a choice of a and b, then using the equation to solve for c.
Case 5: A Satisfies a Rank Condition
The condition may involve the rank of matrix A. The rank of a matrix is the dimension of the vector space generated by its columns (or rows).
Example: Find a 3x3 matrix A such that its rank is 1.
A rank-1 matrix can be expressed as the outer product of two vectors: A = uvᵀ, where 'u' is a 3x1 vector and 'v' is a 1x3 vector. Any choice of 'u' and 'v' (not both zero vectors) will result in a rank-1 matrix A. For example, if u = [1; 0; 0] and v = [1, 2, 3], then A = [[1, 2, 3], [0, 0, 0], [0, 0, 0]].
Advanced Techniques and Considerations
For more complex conditions, more advanced techniques might be required:
- Singular Value Decomposition (SVD): Useful for problems involving matrix norms, rank constraints, or pseudo-inverses.
- Eigenvalue Decomposition: Essential when conditions involve eigenvalues, eigenvectors, or diagonalizability.
- Jordan Normal Form: For matrices that are not diagonalizable.
- Numerical Methods: For large matrices or systems of equations that are difficult to solve analytically.
Conclusion
Finding a matrix A that satisfies a given condition is a versatile problem with applications across numerous fields. The approach hinges on effectively translating the condition into a solvable system of equations or inequalities. By understanding the different types of conditions and the appropriate techniques, you can successfully tackle these problems and apply them to various linear algebra applications. Remember to consider the size and properties of the matrix when choosing your method. Numerical methods might be necessary for very large matrices, while analytical solutions are preferable for smaller, simpler cases. The key is to carefully analyze the "such that" clause and translate it into a workable mathematical framework.
Latest Posts
Latest Posts
-
Mrs Roswell Is A New Medicare Beneficiary
Apr 01, 2025
-
Match Each Description With An Appropriate Ip Address
Apr 01, 2025
-
Advantages Of The Activity Based Costing Include Check All That Apply
Apr 01, 2025
-
Determine The Remaining Sides And Angles Of The Triangle Abc
Apr 01, 2025
-
Correctly Label The Following Internal Anatomy Of The Heart
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Find A Matrix A Such That . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
