Estimate The Following Limit Using Graphs Or Tables.
Holbox
Mar 31, 2025 · 6 min read
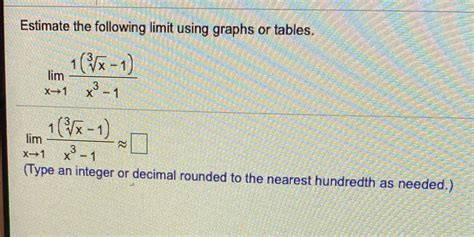
Table of Contents
- Estimate The Following Limit Using Graphs Or Tables.
- Table of Contents
- Estimating Limits Using Graphs and Tables: A Comprehensive Guide
- Understanding Limits Graphically
- Estimating Limits Using Tables
- Combining Graphical and Tabular Methods
- Dealing with Infinite Limits
- Cases Where Limits Don't Exist
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Estimating Limits Using Graphs and Tables: A Comprehensive Guide
Estimating limits is a fundamental concept in calculus. It involves determining the value a function approaches as its input approaches a specific value. While formal limit calculations utilize algebraic manipulation and limit laws, graphical and tabular methods provide intuitive and valuable estimations, particularly when dealing with complex functions or situations where algebraic methods are impractical. This article will delve into the process of estimating limits using graphs and tables, covering various scenarios and offering practical strategies for accurate estimations.
Understanding Limits Graphically
A graph provides a visual representation of a function's behavior. To estimate a limit using a graph, we observe the function's values as the input approaches the target value. The limit exists if the function approaches the same value from both the left and the right sides.
Steps to Estimate a Limit Graphically:
-
Identify the Target Value: Determine the value of x (or the independent variable) for which you need to estimate the limit. Let's denote this value as c.
-
Analyze the Graph Near x = c: Examine the graph's behavior as x approaches c from both the left (values smaller than c) and the right (values larger than c).
-
Observe the y-values: Look at the y-values (or function values) corresponding to the x-values near c. If the y-values approach a single value from both sides, this value is the estimated limit.
-
Consider Asymptotes: If the graph has a vertical asymptote at x = c, the limit may be positive infinity, negative infinity, or it might not exist.
-
Note Discontinuities: If there's a hole or jump in the graph at x = c, the limit might still exist if the function approaches the same value from both sides, even if the function itself is undefined at x = c. The limit describes the value the function approaches, not necessarily the value the function takes on.
Example:
Let's consider the function f(x) = (x² - 4) / (x - 2). We want to estimate the limit as x approaches 2. A graph of this function would reveal a removable discontinuity at x = 2 (a hole). However, as x approaches 2 from both sides, the y-values approach 4. Therefore, we can estimate the limit as:
lim (x→2) [(x² - 4) / (x - 2)] ≈ 4
Limitations of Graphical Estimation:
-
Accuracy: Graphical estimation relies on visual inspection and may not provide highly precise results. The accuracy depends heavily on the scale and resolution of the graph.
-
Complexity: For complex functions or those with subtle behaviors, graphical estimation can be difficult or unreliable.
-
Software Dependence: Creating accurate graphs often requires specialized software or graphing calculators.
Estimating Limits Using Tables
A tabular approach involves creating a table of function values for x-values progressively closer to the target value c. By observing the trend in the y-values, we can estimate the limit.
Steps to Estimate a Limit Using a Table:
-
Choose a Target Value: Identify the x-value (c) for which you need to estimate the limit.
-
Select x-values: Choose a sequence of x-values approaching c from both the left and the right. Start with values relatively far from c, then gradually approach c with increasingly closer values. For example, if c = 2, you might choose x-values like 1.5, 1.8, 1.9, 1.99, 2.01, 2.1, 2.2, 2.5.
-
Calculate y-values: Evaluate the function at each of the selected x-values.
-
Analyze the Trend: Observe the y-values in the table. If the y-values approach a single value as the x-values approach c from both sides, this value is the estimated limit.
-
Consider Patterns: Look for patterns and trends in the y-values. If the differences between consecutive y-values become progressively smaller as x approaches c, it strengthens the estimate's reliability.
Example:
Let's estimate the limit of f(x) = sin(x) / x as x approaches 0 using a table:
| x | f(x) |
|---|---|
| -0.5 | 0.9589 |
| -0.1 | 0.9983 |
| -0.01 | 0.99998 |
| -0.001 | 0.999999 |
| 0.001 | 0.999999 |
| 0.01 | 0.99998 |
| 0.1 | 0.9983 |
| 0.5 | 0.9589 |
From the table, as x approaches 0 from both sides, f(x) approaches 1. Therefore, we can estimate the limit as:
lim (x→0) [sin(x) / x] ≈ 1
Advantages of Tabular Estimation:
-
Systematic Approach: The tabular approach offers a structured and systematic way to analyze function behavior near the target value.
-
Numerical Precision: Tables provide numerical data, offering greater potential for precision than graphical estimations, especially with the use of calculators or computers.
-
Suitable for Complex Functions: Tabular methods are applicable to a wider range of functions, including those whose graphs are difficult to visualize.
Limitations of Tabular Estimation:
-
Computational Effort: Creating a comprehensive table can be time-consuming, especially for complex functions.
-
Limited Precision: While generally more precise than graphical methods, tabular estimations are still limited by the chosen x-values and the accuracy of calculations.
-
Potential for Misinterpretation: Incorrectly chosen x-values or inaccurate calculations can lead to misleading results.
Combining Graphical and Tabular Methods
For enhanced accuracy and understanding, it's often beneficial to combine both graphical and tabular methods. The graph can provide a general overview of the function's behavior, while the table offers a more precise numerical analysis near the target value. This combined approach helps to mitigate the limitations of each method individually.
Dealing with Infinite Limits
When dealing with limits that approach infinity, both graphical and tabular methods can provide insights. Graphically, we examine whether the function values increase without bound (positive infinity) or decrease without bound (negative infinity) as x approaches the target value. In tabular methods, we look for increasingly large positive or negative values in the y-column as the x-values approach the target. Asymptotes play a crucial role in identifying infinite limits.
Cases Where Limits Don't Exist
A limit does not exist if the function approaches different values from the left and right sides of the target value, or if it approaches infinity from one side and negative infinity from the other. Graphical analysis easily reveals such cases by showing distinct approaches from both directions, while tables show discrepancies in the y-values as x approaches the target from the left and right.
Conclusion
Estimating limits using graphs and tables is a valuable skill for understanding the behavior of functions. While not as rigorous as formal limit calculations, these methods offer intuitive and practical estimations, particularly when dealing with complex functions or situations where algebraic methods are difficult to apply. By combining both graphical and tabular approaches, we can achieve greater accuracy and confidence in our limit estimations, solidifying our understanding of this fundamental concept in calculus. Remember that the choice of method often depends on the function's complexity and the desired level of precision.
Latest Posts
Latest Posts
-
Which Code Example Is An Expression
Apr 03, 2025
-
Good Team Goals Are All Of The Following Except
Apr 03, 2025
-
During The Year Trc Corporation Has The Following Inventory Transactions
Apr 03, 2025
-
In Project Network Analysis Slack Refers To The Difference Between
Apr 03, 2025
-
The Economic Way Of Thinking Stresses That
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about Estimate The Following Limit Using Graphs Or Tables. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
