Classify Each Random Variable As Discrete Or Continuous
Holbox
Mar 30, 2025 · 5 min read
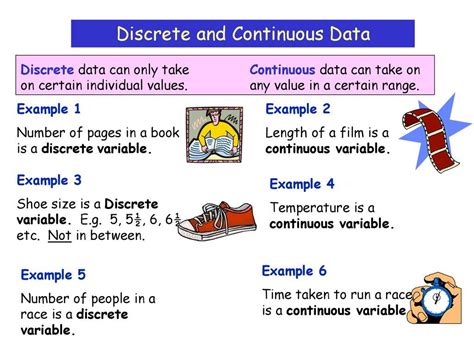
Table of Contents
- Classify Each Random Variable As Discrete Or Continuous
- Table of Contents
- Classify Each Random Variable as Discrete or Continuous: A Comprehensive Guide
- What are Random Variables?
- Discrete vs. Continuous: The Fundamental Difference
- Examples of Discrete Random Variables
- Understanding Count Data: A Key to Discrete Variables
- Examples of Continuous Random Variables
- The Importance of Measurement Precision
- Tricky Cases and Clarifications
- Rounding and Discretization
- Large Numbers and Approximations
- Binary Variables
- Practical Applications and Implications
- Advanced Considerations: Mixed Variables
- Conclusion: Mastering the Classification
- Latest Posts
- Latest Posts
- Related Post
Classify Each Random Variable as Discrete or Continuous: A Comprehensive Guide
Understanding the difference between discrete and continuous random variables is fundamental to mastering probability and statistics. This distinction impacts how we model data, perform calculations, and interpret results. This comprehensive guide will delve into the core concepts, provide clear examples, and equip you with the tools to confidently classify any random variable.
What are Random Variables?
Before diving into the classification, let's establish a firm grasp of what a random variable actually is. A random variable is a variable whose value is a numerical outcome of a random phenomenon. It's a function that maps the outcomes of a random experiment to numerical values. Think of it as a way to quantify uncertainty. For example, if you're flipping a coin, the outcome (heads or tails) isn't inherently numerical. However, we can define a random variable X where X = 1 if the outcome is heads and X = 0 if the outcome is tails. Now we have a numerical representation of the random event.
Discrete vs. Continuous: The Fundamental Difference
The crucial difference lies in the nature of the values a random variable can take:
-
Discrete Random Variable: A discrete random variable can only take on a finite number of values or a countably infinite number of values. These values are often integers, representing counts or distinct categories. The key is that there are gaps between the possible values.
-
Continuous Random Variable: A continuous random variable can take on any value within a given range or interval. There are no gaps between possible values. Think of measuring something like height or weight; you could theoretically measure it to any level of precision.
Let's break down these differences with illustrative examples:
Examples of Discrete Random Variables
Many everyday phenomena lend themselves to discrete random variable modeling:
-
Number of heads in three coin flips: You can have 0, 1, 2, or 3 heads – no other values are possible.
-
Number of cars passing a certain point on a highway in an hour: You can count the cars, and the number will be a whole number.
-
Number of defective items in a batch of 100: Again, you're counting discrete items.
-
The outcome of rolling a die: The possible values are 1, 2, 3, 4, 5, and 6.
-
The number of students in a class: The number of students must be a whole number.
Understanding Count Data: A Key to Discrete Variables
Many discrete variables involve counting things. This is a crucial aspect of recognizing discrete random variables. If the variable represents a count (the number of occurrences of an event), it's highly likely to be discrete.
Examples of Continuous Random Variables
Continuous random variables are often associated with measurements:
-
Height of a person: Height can take on any value within a certain range (e.g., between 4 feet and 7 feet).
-
Weight of a package: The weight can be any value within a certain range.
-
Temperature of a room: Temperature can take on any value within a range.
-
Time taken to complete a task: Time is continuous; you can measure it with arbitrary precision.
-
The length of a piece of string: The length can be any value within a specific range.
The Importance of Measurement Precision
The concept of continuous variables is linked to the idea that you could theoretically measure the variable with increasing precision. While in practice, our measuring tools have limitations, the underlying variable itself isn't restricted to specific values.
Tricky Cases and Clarifications
Some situations can be a bit ambiguous. Let's address potential confusion:
Rounding and Discretization
Sometimes continuous data is rounded to discrete values for practical reasons. For example, we might record someone's height as 5'10" even though their actual height might be 5'10.25". The underlying variable (height) is still continuous, even though the recorded value is discrete.
Large Numbers and Approximations
With very large numbers, the distinction between discrete and continuous can sometimes blur. For instance, the number of grains of sand on a beach is technically discrete, but the number is so vast that treating it as a continuous variable might be a reasonable simplification for certain statistical analyses. The context is crucial here.
Binary Variables
Binary variables (variables that can only take on two values, such as 0 or 1, representing success or failure) are technically discrete. They are a special case of discrete variables with only two possible outcomes.
Practical Applications and Implications
The classification of a random variable has significant implications for statistical analysis:
-
Probability Distributions: Different types of probability distributions are used for discrete and continuous variables. The binomial distribution is a classic example for discrete variables, while the normal distribution is commonly used for continuous variables.
-
Statistical Methods: The choice of statistical methods often depends on whether the variable is discrete or continuous. For example, you would use different methods to calculate the average (mean) for discrete and continuous data.
-
Data Visualization: The way you visualize data depends on whether it's discrete or continuous. Histograms are frequently used for continuous data, while bar charts are more suitable for discrete data.
-
Model Selection: Choosing the appropriate statistical model depends on the nature of your random variables.
Advanced Considerations: Mixed Variables
While the focus is mainly on discrete and continuous, it's worth briefly mentioning the possibility of mixed random variables. These variables exhibit characteristics of both discrete and continuous variables. For instance, consider the amount of rainfall in a day. It could be 0 (no rain), which is discrete, or it could be any positive value (continuous) representing the amount of rainfall.
Conclusion: Mastering the Classification
The ability to classify random variables as discrete or continuous is a cornerstone of statistical thinking. By understanding the underlying concepts and applying them to real-world examples, you'll be able to effectively analyze data, choose appropriate statistical methods, and build robust models to tackle a wide range of problems. Remember to consider the nature of the variable, its possible values, and the context in which it is used to ensure accurate classification. Careful attention to these details will pave your way to successful statistical analyses.
Latest Posts
Latest Posts
-
Which Of The Following Occurs During Data Cleansing
Apr 02, 2025
-
What Was Your First Choice Using The Winre Option Menu
Apr 02, 2025
-
Correctly Label The Following External Anatomy Of The Posterior Heart
Apr 02, 2025
-
Performance Feedback Is Most Effective When It
Apr 02, 2025
-
The Effective Management Of Accounts Receivable Requires Financial Managers To
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Classify Each Random Variable As Discrete Or Continuous . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
