Write The Vector Shown Above In Component Form
Holbox
Mar 30, 2025 · 5 min read
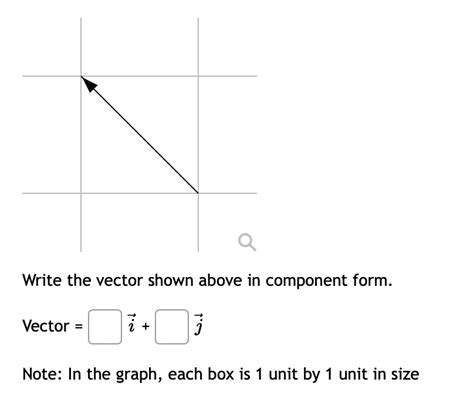
Table of Contents
- Write The Vector Shown Above In Component Form
- Table of Contents
- Writing a Vector in Component Form: A Comprehensive Guide
- What is a Vector?
- Coordinate Systems and Representing Vectors
- Writing a Vector in Component Form: The Process
- Calculating Components from Magnitude and Direction
- Finding the Magnitude and Direction from Component Form
- Vector Addition and Subtraction in Component Form
- Applications of Vectors in Component Form
- Advanced Concepts: Unit Vectors and Basis Vectors
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Writing a Vector in Component Form: A Comprehensive Guide
Understanding how to represent vectors in component form is fundamental to many areas of physics, engineering, and mathematics. This detailed guide will walk you through the process, covering various scenarios and providing ample examples. We’ll explore different coordinate systems, delve into the underlying mathematics, and offer practical tips to ensure accuracy and understanding.
What is a Vector?
Before diving into component form, let's solidify our understanding of vectors themselves. A vector is a mathematical object that possesses both magnitude (size or length) and direction. This contrasts with a scalar, which only has magnitude (e.g., temperature, mass). Vectors are often represented graphically as arrows, where the arrow's length represents the magnitude and its direction, well, the direction of the vector.
Think of examples like displacement (moving from point A to point B), velocity (speed in a specific direction), force (push or pull with a certain strength and direction), and acceleration. All of these are vector quantities.
Coordinate Systems and Representing Vectors
To express a vector numerically, we need a coordinate system. The most common is the Cartesian coordinate system (also known as the rectangular coordinate system), which uses perpendicular x, y, and z axes. Other systems include polar coordinates (using distance and angle) and spherical coordinates (using distance and two angles). For this guide, we'll primarily focus on the Cartesian system.
Within the Cartesian system, we can represent a vector using its components. These components are the projections of the vector onto each axis. For a 2D vector, we have x and y components; for a 3D vector, we have x, y, and z components.
Writing a Vector in Component Form: The Process
Let's say we have a vector v that starts at the origin (0, 0) and ends at the point (a, b) in a 2D Cartesian system. The component form of this vector is written as:
v = <a, b>
Here, 'a' is the x-component and 'b' is the y-component. The angled brackets denote a vector in component form. The x-component represents the vector's projection onto the x-axis, and the y-component represents its projection onto the y-axis.
For a 3D vector originating at (0, 0, 0) and terminating at (a, b, c), the component form is:
v = <a, b, c>
Calculating Components from Magnitude and Direction
Often, we're given the magnitude (||v||) and direction (θ) of a vector, and we need to find its components. We use trigonometry for this. In a 2D system:
- v<sub>x</sub> = ||v|| * cos(θ) (x-component)
- v<sub>y</sub> = ||v|| * sin(θ) (y-component)
Where θ is the angle the vector makes with the positive x-axis (measured counterclockwise).
For a 3D vector, the calculation is more involved and often requires considering angles with respect to each axis, potentially utilizing spherical coordinates or direction cosines. This requires a deeper understanding of vector algebra and trigonometry in three dimensions. The general approach involves decomposing the vector into its projections along each axis using appropriate trigonometric functions.
Example: A vector has a magnitude of 5 units and makes an angle of 30 degrees with the positive x-axis.
v<sub>x</sub> = 5 * cos(30°) = 5 * (√3/2) ≈ 4.33 v<sub>y</sub> = 5 * sin(30°) = 5 * (1/2) = 2.5
Therefore, the component form of the vector is approximately <4.33, 2.5>.
Finding the Magnitude and Direction from Component Form
Given the component form of a vector, we can find its magnitude and direction. In a 2D system:
- ||v|| = √(a² + b²) (Magnitude using Pythagorean theorem)
- θ = tan⁻¹(b/a) (Direction, using the arctangent function)
Remember that the arctangent function (tan⁻¹) only provides an angle within a specific range (-90° to +90°). You need to consider the signs of 'a' and 'b' to determine the correct quadrant for the angle θ.
Example: The vector v = <3, 4>
||v|| = √(3² + 4²) = √25 = 5 θ = tan⁻¹(4/3) ≈ 53.13°
Thus, the magnitude is 5 units, and the direction is approximately 53.13° counterclockwise from the positive x-axis.
For 3D vectors, the magnitude is calculated as:
||v|| = √(a² + b² + c²)
Finding the direction in 3D is more complex and often involves expressing the direction using direction cosines or angles relative to each axis.
Vector Addition and Subtraction in Component Form
One of the significant advantages of using component form is the ease with which vector addition and subtraction can be performed.
Addition: To add two vectors, simply add their corresponding components:
u = <a, b> v = <c, d> u + v = <a + c, b + d>
Subtraction: Subtraction works similarly:
u - v = <a - c, b - d>
This extends seamlessly to 3D vectors. This component-wise addition and subtraction makes vector operations significantly simpler.
Applications of Vectors in Component Form
The component form of vectors finds extensive use in various fields:
- Physics: Analyzing forces, velocities, accelerations, and momentum in mechanics. Describing electric and magnetic fields.
- Engineering: Calculating stresses and strains in structures. Modeling fluid flow. Robotics and computer graphics.
- Computer Graphics: Representing positions, translations, rotations, and scaling of objects. Creating realistic animations and simulations.
- Game Development: Character movement, projectile motion, and collision detection.
Advanced Concepts: Unit Vectors and Basis Vectors
-
Unit Vectors: A unit vector has a magnitude of 1. They are often used to represent directions. In the Cartesian system, the unit vectors along the x, y, and z axes are denoted as i, j, and k, respectively. Any vector can be expressed as a linear combination of these unit vectors.
-
Basis Vectors: A set of linearly independent vectors that can be used to represent any other vector in a given vector space. In the Cartesian system, i, j, and k form a standard basis.
Conclusion
Representing vectors in component form is a powerful tool in mathematics, physics, and computer science. By mastering the techniques outlined in this guide—calculating components from magnitude and direction, finding magnitude and direction from components, performing vector addition and subtraction, and understanding unit and basis vectors—you'll gain a solid foundation for tackling a wide range of vector-related problems. Remember to always clearly define your coordinate system and consistently apply the principles of trigonometry and vector algebra. Practice is key to developing proficiency and intuition when working with vectors in component form. The more you work with vectors in this format, the more natural and intuitive these calculations will become.
Latest Posts
Latest Posts
-
The Policy Of Deterrence Is Based On The Idea That
Apr 02, 2025
-
A Good Ruby Simulant Could Be Made From Spinel
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Write The Vector Shown Above In Component Form . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
