Two Systems Of Equations Are Given Below
Holbox
Apr 02, 2025 · 5 min read
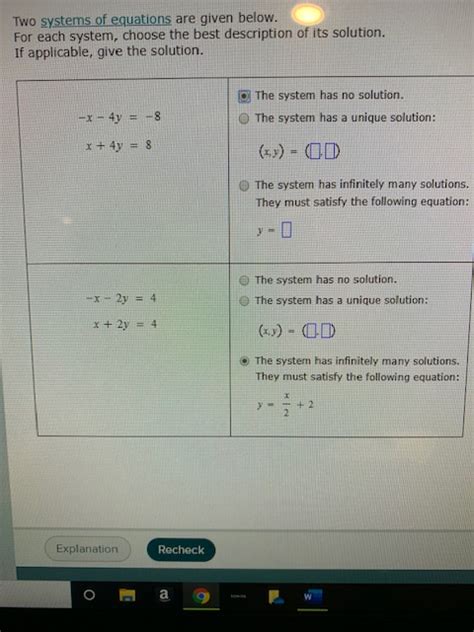
Table of Contents
- Two Systems Of Equations Are Given Below
- Table of Contents
- Two Systems of Equations: A Comprehensive Guide
- Understanding Systems of Equations
- Methods for Solving Linear Systems of Two Equations
- 1. Graphing Method
- 2. Substitution Method
- 3. Elimination Method (Addition/Subtraction Method)
- Solving Non-Linear Systems of Two Equations
- Methods for Non-Linear Systems
- Special Cases and Considerations
- Applications of Systems of Equations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Two Systems of Equations: A Comprehensive Guide
Solving systems of equations is a fundamental concept in algebra with wide-ranging applications in various fields, from physics and engineering to economics and computer science. This article delves deep into the intricacies of solving two systems of equations, exploring different methods, their strengths and weaknesses, and providing illustrative examples to solidify your understanding. We'll cover both linear and non-linear systems, equipping you with a robust toolkit for tackling a variety of problems.
Understanding Systems of Equations
A system of equations is a collection of two or more equations with the same set of unknowns (variables). The goal is to find values for these unknowns that satisfy all the equations simultaneously. In the context of this article, we'll primarily focus on systems with two equations and two unknowns, typically represented as x and y.
Types of Systems:
- Linear Systems: These involve equations where each term is either a constant or a constant multiplied by a single variable raised to the power of 1. They represent straight lines when graphed.
- Non-Linear Systems: These systems contain at least one equation that is not linear. This could involve variables raised to powers other than 1, trigonometric functions, exponential functions, or other non-linear expressions. They can represent curves and lines when graphed.
Methods for Solving Linear Systems of Two Equations
Several methods can efficiently solve linear systems. Let's explore the most common ones:
1. Graphing Method
This method involves graphing both equations on the same coordinate plane. The point of intersection (if one exists) represents the solution to the system.
Advantages: Visually intuitive and easy to understand.
Disadvantages: Not very accurate for solutions involving decimals or fractions. Inefficient for complex systems.
Example:
Solve the system:
x + y = 5
x - y = 1
Graphing these two lines reveals an intersection point at (3, 2). Therefore, x = 3 and y = 2 is the solution.
2. Substitution Method
This method involves solving one equation for one variable in terms of the other, and then substituting this expression into the second equation to solve for the remaining variable.
Advantages: Relatively straightforward and applicable to most linear systems.
Disadvantages: Can become cumbersome with complex expressions.
Example:
Solve the system:
2x + y = 7
x - y = 2
Solve the second equation for x: x = y + 2
Substitute this into the first equation:
2(y + 2) + y = 7
2y + 4 + y = 7
3y = 3
y = 1
Substitute y = 1 back into x = y + 2:
x = 1 + 2 = 3
Therefore, the solution is x = 3 and y = 1.
3. Elimination Method (Addition/Subtraction Method)
This method involves manipulating the equations (multiplying by constants) so that when they are added or subtracted, one variable is eliminated, allowing you to solve for the other.
Advantages: Often the most efficient method, especially for systems with complex coefficients.
Disadvantages: Requires careful attention to algebraic manipulation.
Example:
Solve the system:
3x + 2y = 11
x - 2y = -1
Notice that the y terms have opposite signs and the same coefficient. Adding the two equations eliminates y:
(3x + 2y) + (x - 2y) = 11 + (-1)
4x = 10
x = 2.5
Substitute x = 2.5 into either original equation to solve for y:
2.5 - 2y = -1
2y = 3.5
y = 1.75
Therefore, the solution is x = 2.5 and y = 1.75.
Solving Non-Linear Systems of Two Equations
Solving non-linear systems is more challenging and often requires a combination of methods. There's no single "best" method, and the approach often depends on the specific nature of the equations involved.
Methods for Non-Linear Systems
- Substitution: This remains a powerful technique. Solve one equation for one variable and substitute into the other.
- Elimination: While less common than substitution, elimination can sometimes be applied if appropriate algebraic manipulation is possible.
- Graphing: Graphing is helpful for visualizing the solution but may not yield precise results.
- Numerical Methods: For very complex systems, numerical methods (like iterative techniques) may be necessary.
Example (Substitution):
Solve the system:
x² + y = 4
x + y = 2
Solve the second equation for y: y = 2 - x
Substitute into the first equation:
x² + (2 - x) = 4
x² - x - 2 = 0
This is a quadratic equation. Factoring yields:
(x - 2)(x + 1) = 0
This gives two possible values for x: x = 2 or x = -1.
Substitute each value back into y = 2 - x:
If x = 2, y = 0.
If x = -1, y = 3.
Therefore, the solutions are (2, 0) and (-1, 3).
Special Cases and Considerations
- No Solution: Some systems have no solution. This occurs when the equations represent parallel lines (linear) or curves that do not intersect (non-linear).
- Infinitely Many Solutions: Some systems have infinitely many solutions. This happens when the equations represent the same line (linear) or curves that overlap completely (non-linear).
- Consistent vs. Inconsistent Systems: A consistent system has at least one solution, while an inconsistent system has no solution.
- Dependent vs. Independent Systems: A dependent system has infinitely many solutions, while an independent system has a unique solution.
Applications of Systems of Equations
Systems of equations are essential tools across diverse fields:
- Physics: Solving problems involving motion, forces, and electricity.
- Engineering: Designing structures, analyzing circuits, and modeling systems.
- Economics: Modeling supply and demand, analyzing market equilibrium, and optimizing resource allocation.
- Computer Science: Developing algorithms, solving optimization problems, and creating simulations.
- Chemistry: Solving stoichiometry problems and analyzing chemical reactions.
Conclusion
Mastering the techniques for solving systems of equations, both linear and non-linear, is crucial for success in many academic and professional pursuits. This guide provides a solid foundation for understanding the various methods and their applications. Practice is key to developing proficiency, so work through numerous examples to solidify your understanding and build confidence in tackling complex systems of equations. Remember to always check your solutions by substituting them back into the original equations to ensure they satisfy all the conditions. Understanding the underlying concepts and choosing the most appropriate method will allow you to efficiently and accurately solve a wide variety of problems.
Latest Posts
Latest Posts
-
The Brs Corporation Makes Collections On Sales
Apr 04, 2025
-
Ensuring Data Privacy Is An Essential Skill For Cybersecurity Professionals
Apr 04, 2025
-
Outstanding Common Stock Refers To The Total Number Of Shares
Apr 04, 2025
-
Sales Revenues Are Usually Considered Earned When
Apr 04, 2025
-
The Statement Of Cash Flows Classifies Items As
Apr 04, 2025
Related Post
Thank you for visiting our website which covers about Two Systems Of Equations Are Given Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
