Triangle Congruence Theorems Common Core Geometry Homework Answer Key
Holbox
Mar 30, 2025 · 6 min read
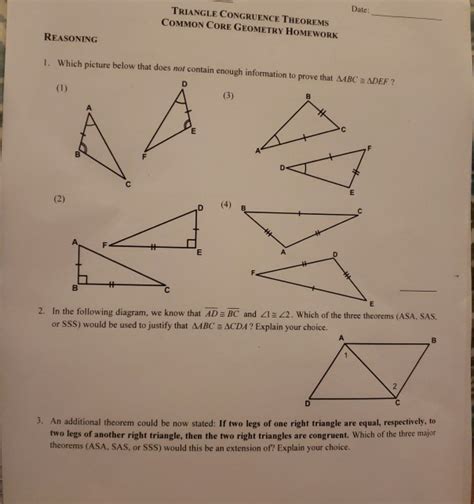
Table of Contents
Triangle Congruence Theorems: Your Comprehensive Guide to Common Core Geometry Homework
Geometry can be a challenging subject, and mastering triangle congruence theorems is a crucial stepping stone to success. This comprehensive guide will delve deep into the five triangle congruence postulates and theorems – SSS, SAS, ASA, AAS, and HL – explaining each one clearly, providing illustrative examples, and offering strategies to tackle common Core Geometry homework problems related to triangle congruence. We'll also explore how to identify congruent triangles in complex diagrams and provide tips for effective study and problem-solving.
Understanding Congruence
Before diving into the theorems, let's establish a solid understanding of what congruence means. Two triangles are considered congruent if they have the same size and shape. This implies that their corresponding sides and angles are equal. Think of it like this: if you could perfectly superimpose one triangle onto the other, they would match exactly. This concept is foundational to many geometric proofs and constructions.
The Five Triangle Congruence Theorems
There are five primary theorems that allow us to definitively prove that two triangles are congruent:
1. Side-Side-Side (SSS) Congruence Postulate:
- Statement: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
- Explanation: This is the most intuitive postulate. If all three sides match in length, the triangles must be identical in shape and size.
- Example: Imagine two triangles, ΔABC and ΔDEF. If AB ≅ DE, BC ≅ EF, and AC ≅ DF, then ΔABC ≅ ΔDEF by SSS.
2. Side-Angle-Side (SAS) Congruence Postulate:
- Statement: If two sides and the included angle of one triangle are congruent to two sides and the included angle of another triangle, then the triangles are congruent.
- Explanation: The "included angle" is the angle formed by the two congruent sides. This postulate emphasizes the importance of the angle's position relative to the sides.
- Example: Consider triangles ΔABC and ΔDEF. If AB ≅ DE, ∠A ≅ ∠D, and AC ≅ DF, then ΔABC ≅ ΔDEF by SAS. Note that ∠A is the included angle between AB and AC.
3. Angle-Side-Angle (ASA) Congruence Postulate:
- Statement: If two angles and the included side of one triangle are congruent to two angles and the included side of another triangle, then the triangles are congruent.
- Explanation: Similar to SAS, the "included side" is crucial. It's the side connecting the two congruent angles.
- Example: In triangles ΔABC and ΔDEF, if ∠A ≅ ∠D, AB ≅ DE, and ∠B ≅ ∠E, then ΔABC ≅ ΔDEF by ASA.
4. Angle-Angle-Side (AAS) Congruence Theorem:
- Statement: If two angles and a non-included side of one triangle are congruent to two angles and the corresponding non-included side of another triangle, then the triangles are congruent.
- Explanation: While seemingly similar to ASA, the key difference is that the congruent side is not between the congruent angles. This theorem is derived from ASA and the Triangle Angle-Sum Theorem (the sum of angles in a triangle is always 180°).
- Example: If in ΔABC and ΔDEF, ∠A ≅ ∠D, ∠B ≅ ∠E, and BC ≅ EF, then ΔABC ≅ ΔDEF by AAS.
5. Hypotenuse-Leg (HL) Congruence Theorem (Right Triangles Only):
- Statement: If the hypotenuse and a leg of one right triangle are congruent to the hypotenuse and a leg of another right triangle, then the triangles are congruent.
- Explanation: This theorem applies only to right triangles. The hypotenuse is the side opposite the right angle, and the leg is one of the other two sides.
- Example: In right triangles ΔABC (where ∠C is the right angle) and ΔDEF (where ∠F is the right angle), if AC ≅ DF (legs) and AB ≅ DE (hypotenuses), then ΔABC ≅ ΔDEF by HL.
Identifying Congruent Triangles in Complex Diagrams
Real-world applications and geometry problems often present more complex diagrams. Here’s a step-by-step approach to identify congruent triangles:
- Isolate the Triangles: Carefully separate the triangles you suspect are congruent from the rest of the diagram. This helps you focus on the relevant information.
- Mark Congruent Parts: Using markings (e.g., tick marks for congruent sides, arcs for congruent angles), systematically label the congruent parts based on the given information.
- Apply the Theorems: Carefully examine the markings you've made. Do they satisfy any of the five congruence postulates or theorems (SSS, SAS, ASA, AAS, HL)?
- Justify Your Conclusion: Clearly state which theorem justifies the congruence. For example, "ΔABC ≅ ΔDEF by ASA."
Common Mistakes to Avoid
- SSA (or ASS): Be aware that there's no SSA or ASS congruence postulate. Two sides and a non-included angle are not sufficient to prove congruence.
- AAA: Having three congruent angles does not guarantee congruence. Triangles with the same angles can have different sizes (similar triangles).
- Incorrect Marking: Double-check your markings to ensure accuracy. A small error in marking can lead to an incorrect conclusion.
- Overlooking Information: Carefully read the problem statement and the diagram to avoid missing crucial information.
Strategies for Solving Common Core Geometry Homework Problems
- Draw and Label Diagrams: A well-drawn and clearly labeled diagram is essential. This makes it easier to visualize the relationships between the triangles and the given information.
- Organize Your Work: Use a systematic approach to solving problems. Write down your reasoning clearly, step by step. This helps you avoid errors and makes it easier to understand your work later.
- Practice Regularly: Consistent practice is key to mastering triangle congruence. Solve a variety of problems, including those with complex diagrams.
- Seek Help When Needed: Don't hesitate to ask for help from your teacher, classmates, or tutors if you're struggling with a particular problem.
Example Problem:
Problem: In the diagram below, AB ≅ DE, BC ≅ EF, and AC ≅ DF. Prove that ΔABC ≅ ΔDEF.
(Diagram would be inserted here showing two triangles, ΔABC and ΔDEF, with corresponding sides labeled as congruent.)
Solution:
Given: AB ≅ DE, BC ≅ EF, AC ≅ DF.
We can directly apply the SSS Congruence Postulate: If three sides of one triangle are congruent to three sides of another triangle, then the triangles are congruent.
Therefore, ΔABC ≅ ΔDEF by SSS.
Advanced Applications and Extensions
Triangle congruence theorems are not just limited to basic geometry problems. They form the basis for many more complex geometric proofs and constructions, including:
- Proofs involving other geometric figures: Congruence theorems are frequently used to prove properties of quadrilaterals, circles, and other shapes.
- Coordinate Geometry: Congruence can be proven using coordinate geometry by calculating distances and slopes.
- Trigonometry: Congruence plays a vital role in establishing trigonometric identities and solving trigonometric equations.
Conclusion
Understanding triangle congruence theorems is essential for success in Common Core Geometry. By mastering the five postulates and theorems (SSS, SAS, ASA, AAS, and HL), practicing regularly, and employing effective problem-solving strategies, you'll build a strong foundation in geometry and confidently tackle complex problems. Remember to always focus on the precise requirements of each theorem, meticulously label your diagrams, and systematically justify your conclusions. With consistent effort and a clear understanding of these concepts, you'll master triangle congruence and excel in your geometry studies.
Latest Posts
Latest Posts
-
Mrs Gonzalez Is Enrolled In Original Medicare
Apr 02, 2025
-
Match The Type Of Reflex With Its Description
Apr 02, 2025
-
Why Is The Term Experimental Psychologist Considered Somewhat Misleading
Apr 02, 2025
-
What Is The Meaning Of Darwins Expression Descent With Modification
Apr 02, 2025
-
Another Term For Return On Investment Is
Apr 02, 2025
Related Post
Thank you for visiting our website which covers about Triangle Congruence Theorems Common Core Geometry Homework Answer Key . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
