The Sum Of 6 Consecutive Odd Numbers Is 204 Sequence
Holbox
May 11, 2025 · 4 min read
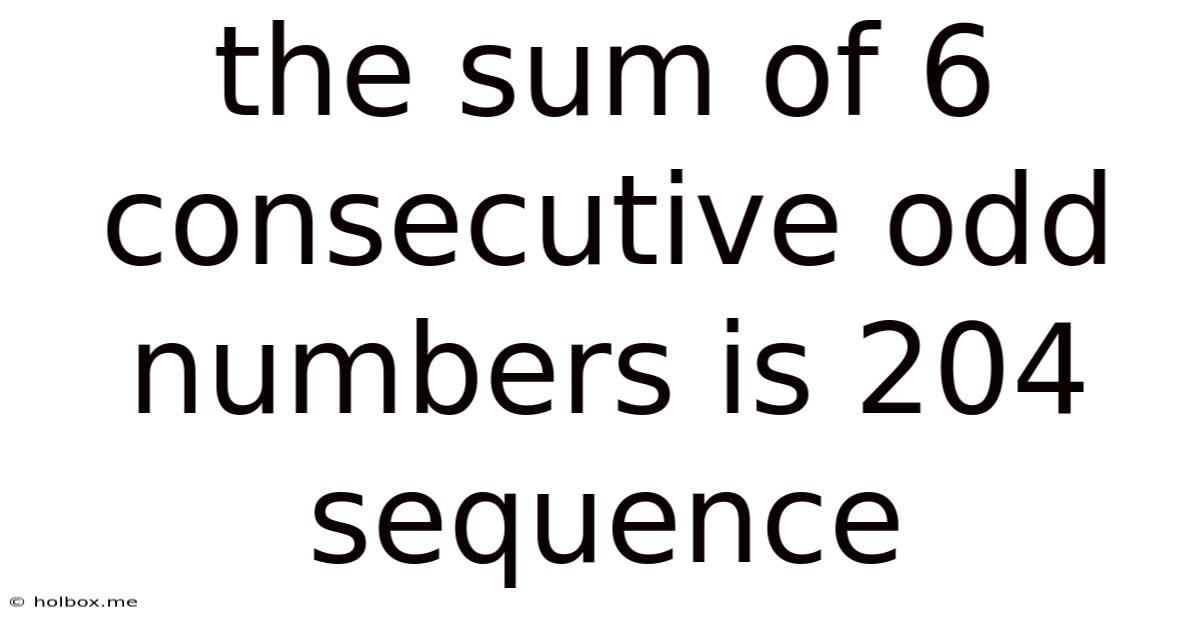
Table of Contents
- The Sum Of 6 Consecutive Odd Numbers Is 204 Sequence
- Table of Contents
- The Sum of 6 Consecutive Odd Numbers is 204: Unraveling the Sequence
- Understanding Arithmetic Sequences
- Method 1: The Algebraic Approach
- Method 2: The Arithmetic Series Formula
- Method 3: Working Backwards from the Average
- Applications of Arithmetic Sequences
- Solving Similar Problems
- Conclusion
- Latest Posts
- Related Post
The Sum of 6 Consecutive Odd Numbers is 204: Unraveling the Sequence
The seemingly simple question, "What are six consecutive odd numbers that add up to 204?" hides a fascinating exploration into arithmetic sequences, algebraic problem-solving, and the power of mathematical reasoning. This article will delve into multiple approaches to solve this problem, explaining the underlying mathematical concepts and providing a step-by-step guide for similar problems. We'll also explore the broader implications of arithmetic sequences and their applications in various fields.
Understanding Arithmetic Sequences
Before we tackle the specific problem, let's establish a firm understanding of arithmetic sequences. An arithmetic sequence is a sequence of numbers such that the difference between any two consecutive terms is constant. This constant difference is called the common difference, often denoted by 'd'. In our case, we are dealing with consecutive odd numbers, meaning the common difference is 2.
Key Characteristics of Arithmetic Sequences:
- Constant Difference: The most defining characteristic is the consistent difference between consecutive terms.
- Predictability: Once you know the first term and the common difference, you can predict any term in the sequence.
- Formulae: Several useful formulas exist to calculate the nth term and the sum of n terms.
Method 1: The Algebraic Approach
This method involves setting up an algebraic equation to represent the problem and then solving for the unknown variable.
1. Defining the Variables:
Let's represent the six consecutive odd numbers as:
- x
- x + 2
- x + 4
- x + 6
- x + 8
- x + 10
Where 'x' represents the smallest odd number in the sequence.
2. Setting up the Equation:
The sum of these six consecutive odd numbers is given as 204. Therefore, we can write the equation:
x + (x + 2) + (x + 4) + (x + 6) + (x + 8) + (x + 10) = 204
3. Solving the Equation:
Simplifying the equation, we get:
6x + 30 = 204
Subtracting 30 from both sides:
6x = 174
Dividing both sides by 6:
x = 29
4. Finding the Sequence:
Now that we know x = 29, we can find the six consecutive odd numbers:
- x = 29
- x + 2 = 31
- x + 4 = 33
- x + 6 = 35
- x + 8 = 37
- x + 10 = 39
Therefore, the sequence is 29, 31, 33, 35, 37, 39.
Method 2: The Arithmetic Series Formula
This method utilizes the formula for the sum of an arithmetic series. The formula is:
S<sub>n</sub> = n/2 * [2a + (n - 1)d]
Where:
- S<sub>n</sub> = the sum of the series
- n = the number of terms
- a = the first term
- d = the common difference
1. Identifying the Variables:
In our problem:
- S<sub>n</sub> = 204
- n = 6
- d = 2
2. Substituting and Solving:
Substituting the known values into the formula:
204 = 6/2 * [2a + (6 - 1)2]
Simplifying:
204 = 3 * [2a + 10]
Dividing both sides by 3:
68 = 2a + 10
Subtracting 10 from both sides:
58 = 2a
Dividing both sides by 2:
a = 29
3. Finding the Sequence:
We now know the first term (a = 29) and the common difference (d = 2). We can easily generate the sequence: 29, 31, 33, 35, 37, 39.
Method 3: Working Backwards from the Average
This method leverages the concept that the average of an arithmetic sequence is the middle term (or the average of the two middle terms if the number of terms is even).
1. Finding the Average:
The average of the six numbers is 204 / 6 = 34.
2. Identifying the Middle Terms:
Since we have an even number of terms, the average is between the third and fourth terms. Therefore, the third and fourth terms are 33 and 35.
3. Constructing the Sequence:
Knowing the third and fourth terms, we can easily construct the entire sequence by subtracting and adding the common difference (2):
29, 31, 33, 35, 37, 39
Applications of Arithmetic Sequences
Arithmetic sequences are far from just a mathematical curiosity. They find practical applications in various fields:
- Finance: Calculating compound interest, analyzing loan repayments, and projecting future investments often involve arithmetic sequences.
- Physics: Modeling uniformly accelerated motion, where the velocity increases at a constant rate, utilizes arithmetic sequences.
- Computer Science: Analyzing algorithms and data structures frequently involves arithmetic sequences.
- Engineering: Designing structures, calculating distances, and planning timelines may utilize arithmetic progressions.
Solving Similar Problems
The methods outlined above can be easily adapted to solve similar problems involving the sum of consecutive odd or even numbers. The key is to:
- Identify the common difference: This will determine the pattern of the sequence.
- Choose an appropriate method: Algebraic equations, the arithmetic series formula, or the average method can all be effective.
- Carefully substitute and solve: Accuracy in calculations is paramount.
Conclusion
The problem of finding six consecutive odd numbers that add up to 204 provides a compelling illustration of the power of mathematical problem-solving. By understanding the principles of arithmetic sequences and employing appropriate methods, we can efficiently and accurately determine the solution. Moreover, this problem highlights the wide-ranging applicability of arithmetic sequences in numerous fields, underscoring their importance in both theoretical mathematics and practical applications. This exploration underscores the beauty and utility of mathematical concepts and their relevance to our daily lives. Remember to practice various problem-solving techniques to enhance your mathematical proficiency and develop a deeper understanding of arithmetic sequences. The more you practice, the easier it will become to tackle similar problems with confidence.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Sum Of 6 Consecutive Odd Numbers Is 204 Sequence . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.