The Graph Of The Relation S Is Shown Below
Holbox
Apr 02, 2025 · 6 min read
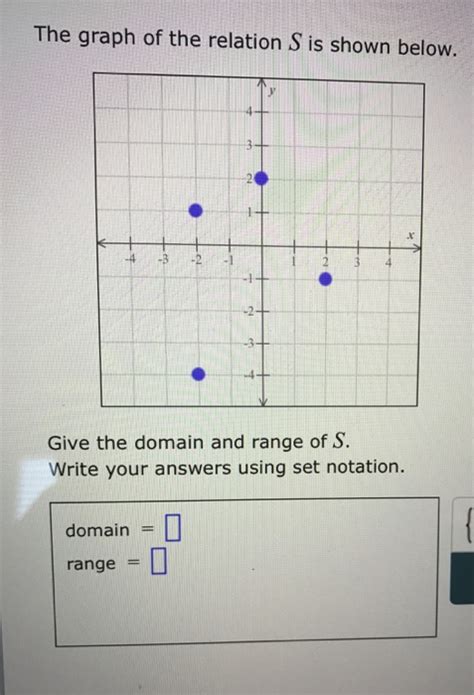
Table of Contents
- The Graph Of The Relation S Is Shown Below
- Table of Contents
- Decoding the Graph: A Comprehensive Analysis of Relation 's'
- Understanding the Fundamentals: Relations and Graphs
- Key Features to Analyze
- Applying the Framework: Examples
- Advanced Considerations and Applications
- Latest Posts
- Latest Posts
- Related Post
Decoding the Graph: A Comprehensive Analysis of Relation 's'
Understanding the relationship depicted in a graph is crucial in various fields, from mathematics and statistics to data science and engineering. This article delves deep into the analysis of a graph representing a relation 's', providing a structured approach to decipher its properties and implications. While I cannot see the specific graph you are referring to, I will provide a framework applicable to diverse graph types, addressing key aspects like domain, range, function characteristics, and potential applications. This comprehensive guide will empower you to analyze any similar graph effectively.
Understanding the Fundamentals: Relations and Graphs
Before diving into the specifics, let's clarify the fundamental concepts. A relation is a set of ordered pairs, where the first element of each pair belongs to a set called the domain, and the second element belongs to a set called the range. The graph visually represents this relation by plotting the ordered pairs as points on a coordinate plane (or a more complex structure for multi-dimensional relations). Each point (x, y) on the graph represents an ordered pair (x, y) in the relation.
Key Features to Analyze
Analyzing a graph requires a methodical approach. Here's a breakdown of crucial aspects to investigate:
- Domain: The set of all possible x-values (input values) represented on the graph. Identify the smallest and largest x-values included in the graph to define the domain's range.
- Range: The set of all possible y-values (output values) represented on the graph. Determine the minimum and maximum y-values to specify the range's extent.
- Type of Relation: Is it a function? A one-to-one function? A many-to-one function? Understanding the type of relation is pivotal in interpreting its properties. A function is a special type of relation where each input (x-value) has only one output (y-value). A one-to-one function further restricts this to ensure each output has only one input. A many-to-one function allows multiple inputs to map to the same output.
- Continuity: Is the graph a continuous curve or a discrete set of points? Continuous graphs represent relations where the variables change smoothly, while discrete graphs show relationships between distinct, separate values.
- Symmetry: Does the graph exhibit any symmetry, such as symmetry about the x-axis, y-axis, or the origin? Symmetry indicates specific relationships within the data.
- Asymptotes: Are there any asymptotes (lines that the graph approaches but never touches)? Asymptotes represent limiting behaviors of the relation.
- Intercepts: Where does the graph intersect the x-axis (x-intercepts) and the y-axis (y-intercepts)? These points represent critical values of the relation.
- Increasing/Decreasing Intervals: Identify the intervals where the graph increases (y-values increase as x-values increase) and decreases (y-values decrease as x-values increase).
- Extrema: Are there any local maxima (highest points in a specific region) or minima (lowest points in a specific region)? Extrema indicate turning points in the relation's behavior.
- Points of Inflection: Identify any points where the concavity of the graph changes (from concave up to concave down or vice versa). These points signify changes in the rate of change of the relation.
Applying the Framework: Examples
Let's consider several hypothetical graph scenarios and apply the analysis framework:
Scenario 1: A Linear Function
Imagine a straight line passing through points (0, 2) and (1, 5).
- Domain: All real numbers (-∞, ∞)
- Range: All real numbers (-∞, ∞)
- Type of Relation: A one-to-one function (linear functions are always functions)
- Continuity: Continuous
- Symmetry: No symmetry
- Asymptotes: None
- x-intercept: The line intersects the x-axis at approximately x = -0.4
- y-intercept: y = 2
- Increasing/Decreasing Intervals: Increasing over the entire domain.
- Extrema: None
- Points of Inflection: None
Scenario 2: A Parabola
Consider a parabola opening upwards with a vertex at (2, 1).
- Domain: All real numbers (-∞, ∞)
- Range: [1, ∞) (y-values are greater than or equal to 1)
- Type of Relation: A many-to-one function (except at the vertex)
- Continuity: Continuous
- Symmetry: Symmetric about the vertical line x = 2
- Asymptotes: None
- x-intercepts: May have 0, 1, or 2 depending on the parabola's equation.
- y-intercept: Depends on the specific equation of the parabola.
- Increasing/Decreasing Intervals: Decreasing for x < 2, increasing for x > 2.
- Extrema: Local minimum at (2, 1)
- Points of Inflection: None
Scenario 3: A Step Function
Consider a step function where y = 1 for 0 ≤ x < 1, y = 2 for 1 ≤ x < 2, and so on.
- Domain: [0, ∞) (or a similar interval depending on the step function's definition)
- Range: {1, 2, 3,...} (a discrete set of integers)
- Type of Relation: A function (each x-value maps to only one y-value)
- Continuity: Discontinuous
- Symmetry: No symmetry
- Asymptotes: May have horizontal asymptotes depending on the function's behavior for large x.
- x-intercepts: None (unless the function is modified)
- y-intercepts: Depends on the specific step function's definition
- Increasing/Decreasing Intervals: Increasing (in a stepwise manner)
- Extrema: None
- Points of Inflection: None
Scenario 4: A Scatter Plot
A scatter plot shows a collection of points without a continuous curve connecting them. Analysis focuses on trends, correlations, and outliers.
- Domain: The range of x-values represented by the plotted points
- Range: The range of y-values represented by the plotted points
- Type of Relation: Generally not a function (unless no two points share the same x-value)
- Continuity: Discontinuous
- Symmetry: May show symmetry depending on data distribution.
- Asymptotes: Not typically relevant
- Intercepts: Dependent on the data points' locations.
- Increasing/Decreasing Intervals: Not directly applicable; instead, look for trends.
- Extrema: Not directly applicable; instead, look for maximum or minimum data points.
- Points of Inflection: Not directly applicable.
Advanced Considerations and Applications
The analysis of a graph extends beyond basic characteristics. More advanced concepts include:
- Derivatives: Calculating the first derivative gives the slope of the graph at any point, indicating the rate of change. The second derivative reveals concavity and points of inflection.
- Integrals: The definite integral over an interval gives the area under the graph, providing insights into accumulated values.
- Regression Analysis: For scatter plots, regression analysis finds the best-fitting line or curve to model the relationship between variables, allowing predictions.
- Differential Equations: Graphs can visualize the solutions to differential equations, which describe dynamic systems.
Real-World Applications
Understanding graph relations finds practical applications in diverse fields:
- Physics: Representing motion, forces, and energy changes over time.
- Engineering: Modeling system behavior, optimizing designs, and predicting performance.
- Economics: Illustrating supply and demand, economic growth, and market trends.
- Biology: Showing population growth, disease spread, and ecological interactions.
- Finance: Visualizing stock prices, investment returns, and risk profiles.
By systematically analyzing the graph of a relation, you uncover valuable information about the underlying relationship between variables, paving the way for informed decisions and a deeper understanding of the data. Remember to always consider the context of the graph and the specific properties relevant to the situation. This comprehensive framework provides a solid foundation for analyzing any relation graph effectively.
Latest Posts
Latest Posts
-
Given The Single Step Reaction Shown Draw The Curved Arrow Mechanism
Apr 05, 2025
-
Which Statement About The Field Of Abnormal Psychology Is Accurate
Apr 05, 2025
-
Cpg Islands Are Associated With Which Of The Following
Apr 05, 2025
-
It Takes 28 Days To Go Around The Earth
Apr 05, 2025
-
Label The Olfactory Receptors And Pathways
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about The Graph Of The Relation S Is Shown Below . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
