The Graph Above Is A Graph Of What Function
Holbox
Mar 27, 2025 · 5 min read
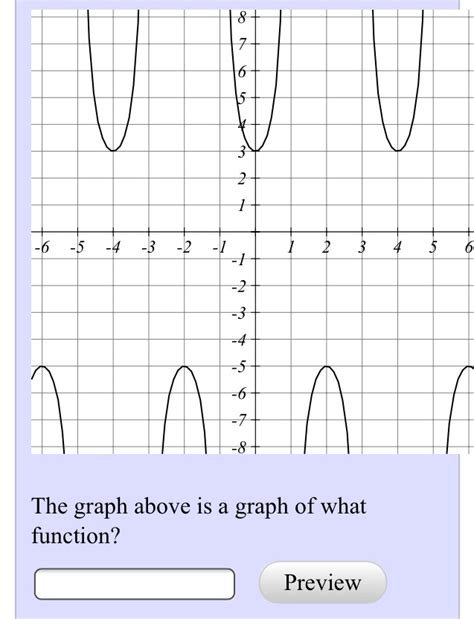
Table of Contents
- The Graph Above Is A Graph Of What Function
- Table of Contents
- Decoding the Graph: Identifying the Underlying Function
- Analyzing the Visual Clues: The First Steps
- Common Function Types and Their Graphical Representations
- Techniques for Function Identification
- The Importance of Context and Further Analysis
- Conclusion: A Iterative Process
- Latest Posts
- Latest Posts
- Related Post
Decoding the Graph: Identifying the Underlying Function
The question "The graph above is a graph of what function?" is a fundamental one in mathematics and data analysis. Without the graph itself, we can only explore the possibilities and the process of identifying the function behind a visual representation. This article will delve into various techniques and considerations for determining the underlying function from a graph, covering a range of function types from simple linear relationships to more complex curves.
Analyzing the Visual Clues: The First Steps
Before jumping into complex mathematical formulas, carefully observing the graph is paramount. Several key features offer crucial clues about the underlying function:
-
Shape: Is the graph a straight line, a parabola (U-shaped), a hyperbola (two separate curves), an exponential curve (rapidly increasing or decreasing), a sinusoidal wave (oscillating), or something else entirely? The overall shape provides the first critical indication of the function type.
-
Intercepts: Where does the graph intersect the x-axis (x-intercepts or roots) and the y-axis (y-intercept)? These points provide specific data points that must satisfy the function's equation. The y-intercept is particularly useful as it represents the function's value when x=0.
-
Asymptotes: Does the graph approach a horizontal or vertical line without ever touching it? These lines are called asymptotes and indicate limitations or restrictions on the function's domain or range. For instance, logarithmic functions have a vertical asymptote, while certain rational functions may have both horizontal and vertical asymptotes.
-
Symmetry: Is the graph symmetrical about the y-axis (even function), the origin (odd function), or neither? Symmetry reveals important properties of the underlying function. Even functions satisfy f(x) = f(-x), while odd functions satisfy f(x) = -f(-x).
-
Turning Points (Extrema): Does the graph have any local maxima (peaks) or minima (valleys)? The number and location of these points provide information about the function's behavior and its derivative (which indicates slope).
-
Continuity: Is the graph a continuous curve, or are there breaks or jumps? Continuous functions can be drawn without lifting your pen from the paper. Discontinuities often indicate piecewise functions or functions with specific restrictions on their domain.
Common Function Types and Their Graphical Representations
Let's explore some frequently encountered function types and their characteristic graphical features:
-
Linear Functions (f(x) = mx + c): These functions are represented by straight lines. The slope 'm' determines the steepness and direction of the line, while 'c' is the y-intercept.
-
Quadratic Functions (f(x) = ax² + bx + c): These functions produce parabolas. The coefficient 'a' determines the parabola's orientation (opens upwards if a>0, downwards if a<0), while the vertex represents the minimum or maximum point.
-
Cubic Functions (f(x) = ax³ + bx² + cx + d): These functions have a more complex S-shaped curve. They can have up to two turning points.
-
Polynomial Functions (f(x) = aₙxⁿ + aₙ₋₁xⁿ⁻¹ + ... + a₁x + a₀): These are generalized forms, encompassing linear, quadratic, cubic, and higher-degree functions. The degree of the polynomial (highest power of x) dictates the maximum number of turning points.
-
Exponential Functions (f(x) = aˣ): These functions exhibit rapid growth or decay. The base 'a' determines the rate of growth (a>1) or decay (0<a<1).
-
Logarithmic Functions (f(x) = logₐ(x)): These functions are the inverse of exponential functions. They have a vertical asymptote at x=0 and slowly increase as x increases.
-
Trigonometric Functions (sin(x), cos(x), tan(x)): These functions produce oscillating waves with specific periods and amplitudes.
-
Rational Functions (f(x) = P(x)/Q(x)): These are functions where both the numerator P(x) and denominator Q(x) are polynomials. They can have asymptotes and discontinuities.
Techniques for Function Identification
Once you've observed the key features of the graph, several approaches can help pinpoint the underlying function:
-
Point-Slope Form for Linear Functions: If the graph is a straight line, use two points (x₁, y₁) and (x₂, y₂) on the line to calculate the slope (m = (y₂ - y₁) / (x₂ - x₁)). Then, use the point-slope form (y - y₁ = m(x - x₁)) to find the equation.
-
Vertex Form for Quadratic Functions: If the graph is a parabola, identify the vertex (h, k) and another point (x, y) on the parabola. Use the vertex form (y - k = a(x - h)²) to find the equation, solving for 'a' using the other point.
-
Regression Analysis: For more complex curves, statistical software or calculators can perform regression analysis. This technique fits various function types to the data points on the graph, providing the best-fitting equation. Common regression types include linear, polynomial, exponential, and logarithmic regressions.
-
Piecewise Functions: If the graph has distinct segments with different characteristics, it likely represents a piecewise function. Determine the function for each segment separately, specifying the domain for each part.
The Importance of Context and Further Analysis
The process of identifying the underlying function from a graph is rarely straightforward. The accuracy and precision depend heavily on the quality of the graph, the available data points, and the context in which the graph is presented.
If you're dealing with real-world data, it’s crucial to understand the context. What does the x-axis represent? What does the y-axis represent? Understanding these variables helps you interpret the function’s meaning and choose the most appropriate model.
Furthermore, advanced mathematical techniques such as calculus (derivatives and integrals) can aid in analyzing the graph’s behavior, identifying critical points, and confirming the function type. For instance, analyzing the slopes at various points can help determine if the function is increasing or decreasing.
Finally, remember that there might not always be a single perfect mathematical function that perfectly matches the graph, especially if the data is noisy or the graph is a visual representation of a complex process. Approximation and model selection are crucial skills in data analysis.
Conclusion: A Iterative Process
Identifying the underlying function of a graph is an iterative process that combines visual observation, mathematical analysis, and contextual understanding. By carefully scrutinizing the graph's characteristics and applying appropriate techniques, you can unveil the mathematical function that describes its shape and behavior. Remember to consider the limitations of your chosen method and always strive for a function that accurately reflects the data and its real-world context. Continuous refinement and critical evaluation are essential for arriving at a robust and insightful conclusion.
Latest Posts
Related Post
Thank you for visiting our website which covers about The Graph Above Is A Graph Of What Function . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
