Simplify This Expression 19 8 14
Holbox
May 13, 2025 · 5 min read
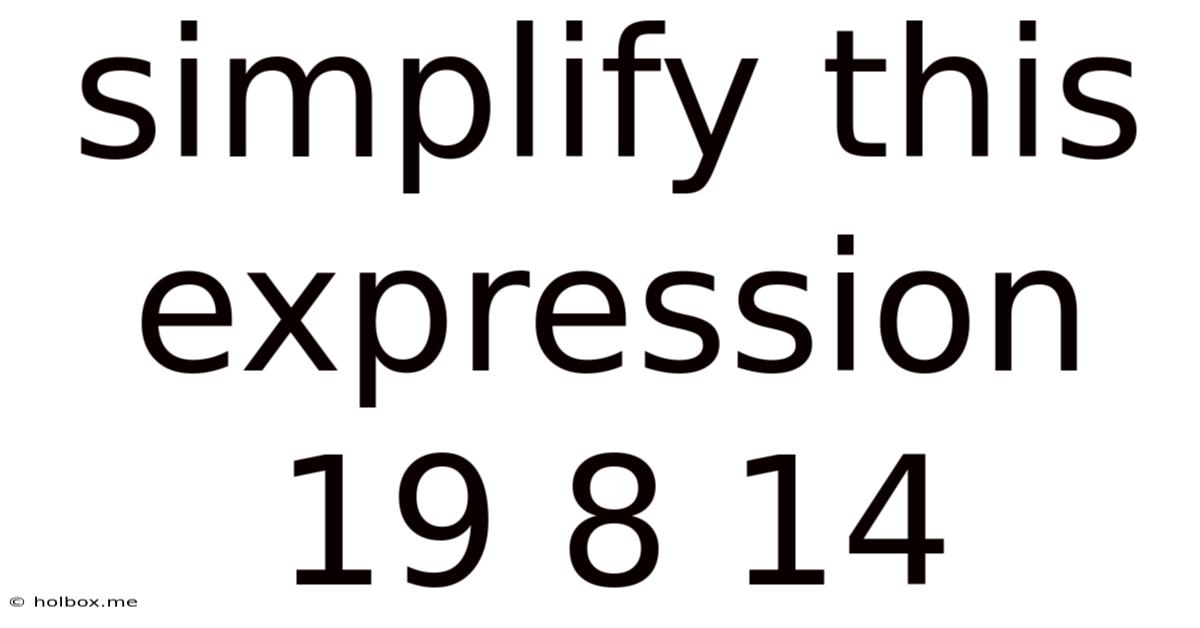
Table of Contents
- Simplify This Expression 19 8 14
- Table of Contents
- Simplifying Mathematical Expressions: A Deep Dive into 19, 8, and 14
- Understanding the Ambiguity: The Importance of Operators
- Possible Interpretations and Simplification
- The Order of Operations (PEMDAS/BODMAS)
- Beyond Basic Arithmetic: Exploring Advanced Concepts
- Practical Applications and Real-World Relevance
- Conclusion: The Value of Clarity in Mathematical Notation
- Latest Posts
- Latest Posts
- Related Post
Simplifying Mathematical Expressions: A Deep Dive into 19, 8, and 14
This article delves into the seemingly simple task of simplifying the expression "19 8 14". While the expression itself lacks explicit operators, understanding its potential interpretations and applying appropriate simplification techniques highlights core mathematical concepts. We'll explore various scenarios, discuss the order of operations (PEMDAS/BODMAS), and demonstrate different methods to arrive at a simplified result. This comprehensive guide is designed to be accessible to a broad audience, from those refreshing their basic arithmetic skills to those seeking a deeper understanding of mathematical notation and simplification.
Understanding the Ambiguity: The Importance of Operators
The expression "19 8 14" is inherently ambiguous because it lacks explicit mathematical operators (+, -, ×, ÷). Without operators, we cannot definitively determine the intended calculation. This underscores the critical importance of precise mathematical notation. To simplify, we must assume the intended operations.
Possible Interpretations and Simplification
Let's explore several plausible interpretations and the resulting simplifications:
1. Addition:
If the expression implies addition, we interpret it as 19 + 8 + 14.
Simplification:
19 + 8 + 14 = 27 + 14 = 41
This is a straightforward addition problem, solvable by adding the numbers sequentially. This interpretation assumes a simple summation of the three numbers.
2. Subtraction (Multiple Interpretations):
Subtraction introduces multiple possibilities due to its non-commutative nature (a - b ≠ b - a).
- Interpretation A: (19 - 8) - 14:
This interpretation involves subtracting 8 from 19, and then subtracting 14 from the result.
Simplification:
(19 - 8) - 14 = 11 - 14 = -3
- Interpretation B: 19 - (8 - 14):
Here, we subtract 14 from 8 first, and then subtract the result from 19.
Simplification:
19 - (8 - 14) = 19 - (-6) = 19 + 6 = 25
- Interpretation C: 19 - 8 - 14:
This involves sequential subtraction.
Simplification:
19 - 8 - 14 = 11 - 14 = -3 (same as Interpretation A)
These examples illustrate the importance of parentheses (or brackets) in clarifying the order of operations when subtraction is involved. Ambiguity can lead to significantly different results.
3. Multiplication:
If the expression implies multiplication, we could interpret it in several ways, depending on whether we treat the numbers as individual factors or as concatenated numbers.
- Interpretation A: 19 × 8 × 14:
This assumes multiplication between each consecutive number.
Simplification:
19 × 8 × 14 = 152 × 14 = 2128
- Interpretation B: 198 × 14:
This interpretation treats "198" as a single number multiplied by 14. This approach requires interpreting the numbers as concatenated digits forming larger numbers.
Simplification:
198 × 14 = 2772
This highlights the significant difference in outcome based on how the expression is interpreted. The context is crucial in such situations.
4. Mixed Operations:
More complex scenarios involve a mix of operations. Without explicit operators or parentheses, the order of operations is undefined, making the simplification highly subjective. For instance, we could assume a combination of addition and subtraction or addition and multiplication, leading to various possible outcomes.
The Order of Operations (PEMDAS/BODMAS)
The order of operations, often remembered by the acronyms PEMDAS (Parentheses, Exponents, Multiplication and Division, Addition and Subtraction) or BODMAS (Brackets, Orders, Division and Multiplication, Addition and Subtraction), is a critical concept in mathematical simplification. These mnemonics dictate the sequence in which operations should be performed:
- Parentheses/Brackets: Operations within parentheses or brackets are performed first.
- Exponents/Orders: Exponents (powers) and roots are evaluated next.
- Multiplication and Division: These operations are performed from left to right.
- Addition and Subtraction: These are performed from left to right.
Without parentheses or any other operators, applying PEMDAS/BODMAS directly to "19 8 14" is not possible. The ambiguity remains unless we impose an operational interpretation.
Beyond Basic Arithmetic: Exploring Advanced Concepts
While "19 8 14" primarily deals with basic arithmetic, the underlying issues of ambiguity and the importance of precise notation extend to more advanced mathematical concepts. For example:
- Matrix Algebra: In matrix algebra, the juxtaposition of numbers could represent matrix multiplication (if 19, 8, and 14 were elements within matrices), which would necessitate a different set of simplification rules.
- Abstract Algebra: In abstract algebra, the expression might represent elements in a group or ring, and the simplification would depend on the defined operations within that algebraic structure.
- Programming Languages: In programming, similar ambiguous expressions require explicit use of operators and parentheses to ensure unambiguous execution.
These examples highlight that the seeming simplicity of "19 8 14" masks deeper mathematical considerations.
Practical Applications and Real-World Relevance
While seemingly abstract, the principles involved in simplifying expressions have extensive practical applications:
- Data Analysis: Correct order of operations and accurate interpretation of mathematical expressions are fundamental to data analysis. Incorrect interpretation can lead to erroneous conclusions.
- Engineering: Engineering calculations across various disciplines (civil, mechanical, electrical) rely on precise mathematical notation and the correct application of order of operations.
- Finance: Financial calculations, such as compound interest calculations or portfolio analysis, necessitate the accurate use of mathematical expressions.
- Computer Science: In programming, understanding order of operations is crucial for writing correct and efficient code. Ambiguous expressions can lead to runtime errors or unexpected program behavior.
The ability to accurately simplify even simple expressions is a foundational skill applicable across numerous fields.
Conclusion: The Value of Clarity in Mathematical Notation
The seemingly trivial expression "19 8 14" serves as a powerful illustration of the crucial role of clear and unambiguous mathematical notation. The lack of explicit operators highlights the potential for misinterpretations and underscores the necessity for precise communication in mathematics and related fields. By examining different interpretations and applying the order of operations, we’ve shown how seemingly simple expressions can lead to drastically different results. This exercise reinforces the importance of consistent and careful mathematical practice to avoid errors and ensure accuracy in any context where mathematical operations are involved. Mastering these basic skills forms a strong foundation for tackling more complex mathematical challenges.
Latest Posts
Latest Posts
-
How Much Is 18 Stone In Pounds
May 20, 2025
-
How Many Weeks Is 16 Days
May 20, 2025
-
How Many Seconds Are In 90 Minutes
May 20, 2025
-
How Many Minutes Are In 48 Hours
May 20, 2025
-
What Is 69 Cm In Inches
May 20, 2025
Related Post
Thank you for visiting our website which covers about Simplify This Expression 19 8 14 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.