Selections Made With Replacement Are Considered To Be
Holbox
Apr 02, 2025 · 7 min read
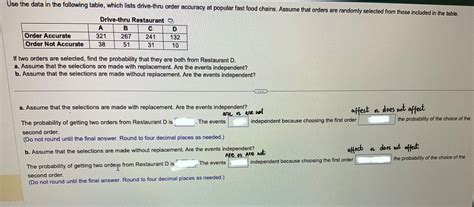
Table of Contents
- Selections Made With Replacement Are Considered To Be
- Table of Contents
- Selections Made With Replacement Are Considered to Be: Independent Events and Their Implications
- What are Independent Events?
- Selections with Replacement: The Core Concept
- Calculating Probabilities with Replacement
- Applications of Selections with Replacement
- 1. Probability and Statistics:
- 2. Computer Science and Data Structures:
- 3. Everyday Decision Making:
- Selections Without Replacement: A Key Distinction
- Hypergeometric Distribution: Selections Without Replacement
- Implications of Choosing the Right Model
- Beyond Basic Scenarios: More Complex Applications
- Practical Considerations and Error Avoidance
- Conclusion: The Significance of Independence
- Latest Posts
- Latest Posts
- Related Post
Selections Made With Replacement Are Considered to Be: Independent Events and Their Implications
Selections made with replacement are considered to be independent events. This seemingly simple concept has profound implications across various fields, from probability theory and statistics to computer science and even everyday decision-making. Understanding this principle is crucial for accurate calculations and informed choices. This article delves deep into the nature of selections with replacement, exploring its characteristics, applications, and contrasts with selections without replacement.
What are Independent Events?
Before diving into selections with replacement, let's clarify the meaning of independent events. Two events are considered independent if the occurrence of one event does not affect the probability of the other event occurring. In simpler terms, the outcome of one event doesn't influence the outcome of the other. For example, flipping a coin twice are independent events; the result of the first flip (heads or tails) doesn't change the probability of getting heads or tails on the second flip.
Selections with Replacement: The Core Concept
In selections with replacement, we choose items from a set, and after each selection, we return the selected item to the set. This ensures that the composition of the set remains unchanged throughout the process. Each selection is completely independent of the others because the probability of selecting any particular item remains constant throughout.
Consider drawing marbles from a bag. If we draw a red marble, and then replace it before drawing again, the probability of drawing a red marble on the second draw is exactly the same as it was on the first draw. This contrasts sharply with selections without replacement, which we'll discuss later.
Calculating Probabilities with Replacement
The key to calculating probabilities in selections with replacement is understanding that each selection is an independent event. This means we can use the multiplication rule for independent events: the probability of a sequence of independent events is the product of their individual probabilities.
Example:
Let's say we have a bag with 5 red marbles and 3 blue marbles. We draw a marble, replace it, and draw again. What's the probability of drawing two red marbles?
- Probability of drawing a red marble on the first draw: 5/8 (5 red marbles out of 8 total marbles)
- Probability of drawing a red marble on the second draw: 5/8 (since we replaced the marble, the probabilities remain the same)
- Probability of drawing two red marbles: (5/8) * (5/8) = 25/64
This simple calculation illustrates the power of independence. We can easily extend this principle to any number of selections with replacement.
Applications of Selections with Replacement
The concept of independent events and selections with replacement has wide-ranging applications:
1. Probability and Statistics:
-
Binomial Distribution: The binomial distribution, a fundamental concept in probability, is directly related to selections with replacement. It models the probability of getting a certain number of "successes" in a fixed number of independent trials, where each trial has the same probability of success. Examples include the probability of getting a certain number of heads in multiple coin flips or the probability of a certain number of defective items in a sample from a production line.
-
Monte Carlo Simulations: Monte Carlo simulations use random sampling to model various phenomena. Often, these simulations involve selections with replacement, especially when the samples need to maintain a constant probability distribution.
2. Computer Science and Data Structures:
-
Random Number Generation: Many algorithms rely on generating sequences of random numbers. These numbers are often generated as if they were selected with replacement from a finite set of numbers, ensuring independence between the generated values.
-
Hashing: Hashing algorithms, used extensively in data structures like hash tables, often treat the input data as if it were selected with replacement. The collisions (two different inputs hashing to the same value) are essentially probabilistic events that can be analyzed using the principles of selections with replacement.
3. Everyday Decision Making:
While not as explicitly mathematical, many everyday scenarios mirror selections with replacement. For example, repeatedly trying to unlock a door with a key (putting the key back after each attempt) is analogous to selections with replacement. The success or failure of each attempt is an independent event.
Selections Without Replacement: A Key Distinction
It's crucial to contrast selections with replacement with selections without replacement. In selections without replacement, we do not return the selected item to the set. This dramatically changes the probability of subsequent selections. Each selection affects the composition of the remaining set, leading to dependent events.
Example:
Using the same bag of 5 red and 3 blue marbles, let's draw two marbles without replacement. The probability of drawing a red marble on the first draw is still 5/8. However, the probability of drawing a red marble on the second draw depends on the outcome of the first draw:
- If the first draw was red: The probability of drawing a red marble on the second draw is 4/7 (4 red marbles left out of 7 total marbles).
- If the first draw was blue: The probability of drawing a red marble on the second draw is 5/7 (5 red marbles left out of 7 total marbles).
The probabilities are interconnected and dependent. We cannot simply multiply the individual probabilities like we did with replacement. Instead, we need to use conditional probability.
Hypergeometric Distribution: Selections Without Replacement
The probability distribution relevant to selections without replacement is the hypergeometric distribution. This distribution models the probability of drawing a certain number of successes in a fixed number of draws without replacement from a finite population. It incorporates the dependencies between draws. The hypergeometric distribution is more complex than the binomial distribution due to these dependencies.
Implications of Choosing the Right Model
The choice between using the binomial distribution (for selections with replacement) and the hypergeometric distribution (for selections without replacement) is crucial for accurate probability calculations. Using the wrong model can lead to significant errors in estimations and predictions. Careful consideration of whether the sampling process involves replacement is therefore essential.
Beyond Basic Scenarios: More Complex Applications
The principles of selections with replacement extend beyond basic examples. Consider these more sophisticated scenarios:
-
Sampling with Replacement in Surveys: Many surveys utilize stratified sampling. In this method, the population is divided into subgroups (strata), and samples are drawn from each stratum. Often, sampling is done with replacement within each stratum to ensure that the sample accurately represents the proportions in the stratum.
-
Bootstrap Resampling: The bootstrap method, a powerful resampling technique used in statistics, involves repeatedly sampling from a dataset with replacement. This creates multiple simulated datasets that can be used to estimate statistical properties like confidence intervals.
-
Markov Chains: Markov chains model systems that transition between states probabilistically. The transition probabilities often represent selections with replacement, where the probability of moving from one state to another is independent of how the system arrived at its current state.
Practical Considerations and Error Avoidance
When working with selections with replacement, it's easy to make mistakes if the fundamental principles are not clearly understood. Here are some key points to consider:
-
Clearly Define the Selection Process: Always explicitly state whether the selection is with or without replacement. Ambiguity can lead to significant errors.
-
Verify Independence: Before applying the multiplication rule for independent events, ensure that the events truly are independent. This is particularly important in complex scenarios.
-
Use the Correct Probability Distribution: Choose the appropriate probability distribution (binomial for with replacement, hypergeometric for without replacement) based on the sampling process.
-
Consider Sample Size: While the binomial distribution is accurate for any sample size with replacement, the accuracy of approximations (like using the normal distribution to approximate the binomial) can be affected by sample size.
Conclusion: The Significance of Independence
Selections made with replacement are characterized by the independence of each event. This fundamental property simplifies probability calculations and allows us to use the powerful binomial distribution to model a wide range of phenomena. Understanding the distinction between selections with and without replacement is crucial for accurate probabilistic modeling and informed decision-making across numerous fields. By mastering this core concept, you unlock the ability to perform more accurate analyses and solve a wide variety of problems involving probability and statistics. Remember to always carefully consider the context of your problem to ensure you're using the correct models and avoiding common errors.
Latest Posts
Latest Posts
-
A Plastic Ocean Documentary Companion Questions
Apr 05, 2025
-
Which Of These Boating Activities Violates Homeland Security Restrictions
Apr 05, 2025
-
The Following Transactions Are From Ohlm Company
Apr 05, 2025
-
Use The Reaction Above To Fill In The Sentences Below
Apr 05, 2025
-
Kendra Is Researching The Effects Of Vitamin C
Apr 05, 2025
Related Post
Thank you for visiting our website which covers about Selections Made With Replacement Are Considered To Be . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
