Select All Vectors With An X Component Of Zero
Holbox
Mar 28, 2025 · 6 min read
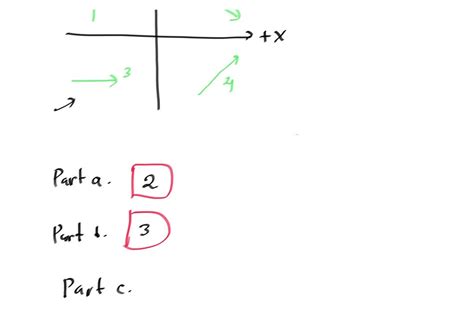
Table of Contents
- Select All Vectors With An X Component Of Zero
- Table of Contents
- Selecting All Vectors with an x-Component of Zero: A Comprehensive Guide
- What are Vectors?
- 1. Geometric Representation:
- 2. Component Representation:
- Identifying Vectors with a Zero x-Component
- Mathematical Representations and Operations
- 2D Vectors:
- 3D Vectors:
- Vector Operations:
- Applications in Different Fields
- 1. Physics:
- 2. Computer Graphics:
- 3. Game Development:
- Selecting Vectors Programmatically
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Selecting All Vectors with an x-Component of Zero: A Comprehensive Guide
Understanding vectors and their components is fundamental in physics, mathematics, and computer graphics. This article dives deep into the concept of vectors, specifically focusing on how to identify and select vectors possessing a zero x-component. We'll explore various representations of vectors, delve into practical applications, and provide illustrative examples to solidify your understanding.
What are Vectors?
Before we zero in on vectors with a zero x-component, let's establish a solid foundation. A vector is a mathematical object that has both magnitude (size or length) and direction. Unlike scalars, which only have magnitude (e.g., temperature, mass), vectors represent quantities with both magnitude and direction. This makes them ideal for representing physical quantities like force, velocity, and acceleration.
Vectors can be represented in several ways:
1. Geometric Representation:
This is the most intuitive way to visualize a vector. It's represented as an arrow where the length of the arrow represents the magnitude, and the direction the arrow points represents the direction of the vector. The starting point of the arrow is called the tail, and the ending point is called the head.
2. Component Representation:
This representation breaks down the vector into its components along the coordinate axes (typically x, y, and z in three dimensions). For example, a 2D vector v can be represented as v = (x, y), where 'x' is the x-component and 'y' is the y-component. Similarly, a 3D vector would be represented as v = (x, y, z). This component form is crucial for mathematical operations on vectors.
Identifying Vectors with a Zero x-Component
The core of this article focuses on identifying vectors where the x-component is equal to zero. In a 2D Cartesian coordinate system, such vectors lie entirely along the y-axis. In a 3D Cartesian coordinate system, they lie within the yz-plane.
Key characteristics of these vectors:
- Zero x-component: This is the defining characteristic. The value representing the x-component is precisely zero.
- Direction: The direction is purely determined by the y and z components (if applicable). The vector points either in the positive or negative direction of the y-axis (in 2D) or within the yz-plane (in 3D).
- Magnitude: The magnitude is calculated using the Pythagorean theorem (or its 3D equivalent). For a 2D vector (0, y), the magnitude is simply |y|. For a 3D vector (0, y, z), the magnitude is √(y² + z²).
Mathematical Representations and Operations
Let's explore how to represent and manipulate these vectors mathematically.
2D Vectors:
A 2D vector with a zero x-component can be generically written as: v = (0, y), where 'y' can be any real number (positive, negative, or zero).
Examples:
- v = (0, 5): A vector with magnitude 5 pointing in the positive y-direction.
- v = (0, -3): A vector with magnitude 3 pointing in the negative y-direction.
- v = (0, 0): The zero vector, having zero magnitude and no defined direction.
3D Vectors:
In three dimensions, vectors with a zero x-component have the form: v = (0, y, z), where 'y' and 'z' can be any real numbers.
Examples:
- v = (0, 2, 4): A vector pointing in the positive y and z directions.
- v = (0, -1, 3): A vector pointing in the negative y and positive z directions.
- v = (0, 0, 7): A vector pointing in the positive z-direction.
Vector Operations:
Standard vector operations like addition, subtraction, scalar multiplication, and dot product can be applied to these vectors. Remember that the x-component will remain zero after many operations (excluding operations that explicitly modify the x-component). For instance:
- Addition: (0, y₁, z₁) + (0, y₂, z₂) = (0, y₁ + y₂, z₁ + z₂)
- Subtraction: (0, y₁, z₁) - (0, y₂, z₂) = (0, y₁ - y₂, z₁ - z₂)
- Scalar Multiplication: k(0, y, z) = (0, ky, kz)
Applications in Different Fields
Vectors with zero x-components appear in numerous applications across diverse fields:
1. Physics:
- Projectile Motion: When analyzing projectile motion, if we choose the x-axis to align with the horizontal direction, the vertical component of the velocity and acceleration vectors will have zero x-components.
- Forces: Consider forces acting purely vertically (gravity, for example). If we set up a coordinate system with x as the horizontal direction, the force vector will have a zero x-component.
- Electromagnetism: In certain electromagnetic scenarios, field vectors might have zero x-components depending on the configuration of charges and currents.
2. Computer Graphics:
- 2D Transformations: Transformations along the y-axis in 2D graphics involve vectors with a zero x-component. This is especially pertinent in rotations around the y-axis and translations purely along the y-axis.
- 3D Modeling: Similar to 2D, manipulations in 3D modeling that concern the yz-plane often involve vectors with x-components of zero.
3. Game Development:
- Character Movement: If a character in a game moves only along the y-axis (e.g., jumping), the velocity vector will have a zero x-component.
- Camera Control: Controlling a game camera by panning vertically results in a camera movement vector with a zero x-component.
Selecting Vectors Programmatically
In programming, selecting vectors with a zero x-component involves checking the x-component of each vector in a dataset or array. The specific implementation would depend on the programming language. Here are some general concepts using pseudo-code:
function selectZeroXComponentVectors(vectors):
selectedVectors = []
for each vector in vectors:
if vector.x == 0:
append vector to selectedVectors
return selectedVectors
This function iterates through a list of vectors and adds only those with an x-component of zero to a new list. The specific implementation will need to adapt to how your programming language represents vectors (e.g., as arrays, tuples, or custom classes). Error handling (for null or undefined vectors) might also need to be incorporated in a production-ready version.
Conclusion
Understanding and selecting vectors with a zero x-component is a crucial skill in many areas of science, engineering, and computer science. This article has comprehensively explored various aspects of these vectors, from their mathematical representation and operations to practical applications in different fields. This foundation will empower you to confidently work with vectors and utilize their properties in various computational and analytical scenarios. Remember that choosing the appropriate coordinate system is critical in correctly identifying vectors with zero x-components. The selection method and its applications depend heavily on the specific problem context. Keep practicing, and you'll become proficient in handling these fundamental mathematical objects.
Latest Posts
Latest Posts
-
Which Of The Following Statements About Menopause Is True
Mar 31, 2025
-
Monetary Policy Refers To The Actions The
Mar 31, 2025
-
What Value Of N Makes The Equation True
Mar 31, 2025
-
Which Region Of The Ear Houses Perilymph And Endolymph
Mar 31, 2025
-
Express Your Answer As A Signed Integer
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Select All Vectors With An X Component Of Zero . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
