Pr 9x 31 And Qr 43 Find X
Holbox
Apr 27, 2025 · 5 min read
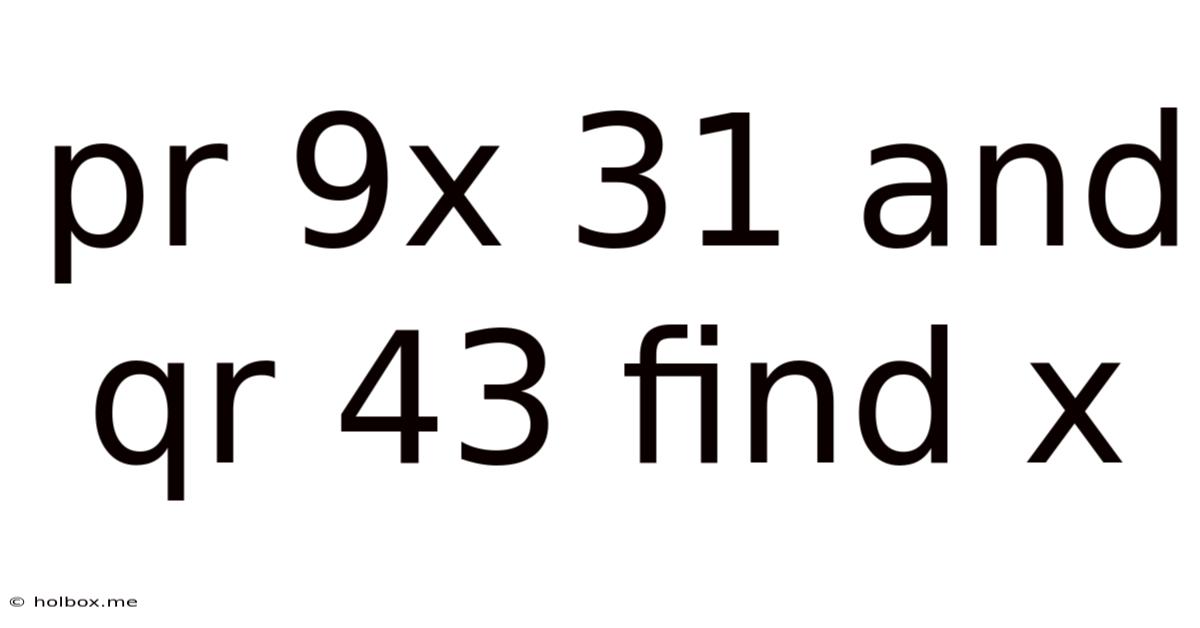
Table of Contents
- Pr 9x 31 And Qr 43 Find X
- Table of Contents
- Solving for x: Exploring the Equations PR 9x + 31 and QR 43
- Understanding the Problem: PR = 9x + 31 and QR = 43
- Scenario 1: PR and QR Represent Equal Lengths
- Scenario 2: PR and QR are Related Through a Proportion or Ratio
- Scenario 3: PR and QR are Parts of a Geometric Figure
- Scenario 4: PR and QR Represent Different Quantities Altogether
- Advanced Concepts and Mathematical Extensions
- Linear Equations and Their Solutions
- Graphical Representation
- Systems of Equations
- Inequalities
- Importance of Context and Clear Problem Definition
- Practical Applications and Further Exploration
- Latest Posts
- Latest Posts
- Related Post
Solving for x: Exploring the Equations PR 9x + 31 and QR 43
This article delves into the mathematical puzzle of solving for 'x' in the given equations, exploring different approaches, and providing a comprehensive understanding of the underlying principles. We'll unpack the problem, examine potential solutions, and discuss the broader mathematical concepts involved. The core problem presented is to find the value of 'x' when we have two expressions involving 'x': PR = 9x + 31 and QR = 43. While the problem statement itself is concise, it opens the door to a number of interpretations and solution strategies depending on the relationship between PR and QR. Let's explore them.
Understanding the Problem: PR = 9x + 31 and QR = 43
The heart of the problem lies in the ambiguity of the notation. 'PR' and 'QR' are typically used in geometry to represent line segments or distances. If we consider this geometric interpretation, the problem might involve finding 'x' based on the lengths of segments PR and QR. However, without further context regarding the relationship between these segments (e.g., are they equal, is one a multiple of the other, are they part of a larger geometric figure?), we can’t directly solve for 'x'. The provided information is insufficient to provide a definitive, singular solution.
Let's explore the different possible scenarios and the approaches needed to solve for 'x' under each scenario.
Scenario 1: PR and QR Represent Equal Lengths
If we assume PR and QR represent line segments of equal length, we can set up an equation:
9x + 31 = 43
This is a simple linear equation. Solving for 'x' involves isolating the variable:
- Subtract 31 from both sides: 9x = 43 - 31 => 9x = 12
- Divide both sides by 9: x = 12/9 => x = 4/3 or 1.333...
In this scenario, the value of x that makes PR and QR equal is 4/3 or approximately 1.333.
Scenario 2: PR and QR are Related Through a Proportion or Ratio
If PR and QR are related through a specific ratio or proportion, the solution method would differ. For example, if PR is twice the length of QR, the equation would be:
9x + 31 = 2 * 43
Solving this equation:
- Simplify the right side: 9x + 31 = 86
- Subtract 31 from both sides: 9x = 55
- Divide both sides by 9: x = 55/9 or approximately 6.111...
In this case, assuming PR is twice QR, x is approximately 6.111. Different ratios would yield different values of x.
Scenario 3: PR and QR are Parts of a Geometric Figure
If PR and QR are parts of a larger geometric figure (triangle, quadrilateral, etc.), the solution would depend on the properties of that figure and the relationships between its sides and angles. We might need additional information, such as angles or other side lengths, to establish the relationships and solve for 'x'. For instance, if PR and QR are sides of a right-angled triangle, the Pythagorean theorem might be applicable.
Scenario 4: PR and QR Represent Different Quantities Altogether
The labels 'PR' and 'QR' might not represent geometric quantities. They could be variables in a different context entirely – perhaps representing physical quantities (e.g., pressure and resistance in an electrical circuit) or abstract quantities in a model. In this case, the nature of the relationship between PR and QR would be crucial in determining the solution for 'x'. We would need a clear statement of how PR and QR are related to solve for x.
Advanced Concepts and Mathematical Extensions
The simple equation derived in Scenario 1 allows us to explore more complex mathematical concepts.
Linear Equations and Their Solutions
The equation 9x + 31 = 43 is a prime example of a linear equation. Linear equations are characterized by their first-degree polynomials. The general form is ax + b = c, where 'a', 'b', and 'c' are constants, and 'x' is the variable to be solved for. Solving these equations always involves isolating the variable through algebraic manipulation (addition, subtraction, multiplication, and division).
Graphical Representation
Linear equations can be easily graphed on a Cartesian coordinate system. The graph of 9x + 31 = 43 is a horizontal line at y = 43. The solution, x = 4/3, is the x-coordinate of the point where this horizontal line intersects the line representing the equation 9x + 31.
Systems of Equations
If we were given additional information relating PR and QR, we might need to solve a system of equations. A system of equations involves two or more equations with the same variables. Solving a system of equations means finding the values of the variables that satisfy all equations simultaneously. Various methods exist for solving systems of equations, such as substitution, elimination, and matrix methods.
Inequalities
Instead of equality, we could have inequalities. For example, if PR > QR, we would have:
9x + 31 > 43
Solving this inequality:
- Subtract 31 from both sides: 9x > 12
- Divide both sides by 9: x > 4/3
This means x must be greater than 4/3 to satisfy the inequality.
Importance of Context and Clear Problem Definition
The core takeaway from this exploration is the paramount importance of context and a clearly defined problem statement. The initial problem, "PR 9x + 31 and QR 43 find x," is insufficient to produce a definitive answer. We need additional information to understand the relationship between PR and QR to find a solution for 'x'. This highlights the crucial role of precision and thoroughness in formulating mathematical problems. Ambiguity can lead to multiple interpretations and solutions, emphasizing the need for clear communication in mathematics and other problem-solving domains.
Practical Applications and Further Exploration
The techniques used to solve for 'x' in these scenarios have wide-ranging applications in various fields. Linear equations, systems of equations, and inequalities are foundational tools used in:
- Engineering: Calculating forces, stresses, and strains in structures.
- Physics: Modeling motion, energy, and other physical phenomena.
- Economics: Predicting market trends, analyzing costs and profits.
- Computer science: Algorithm design and optimization.
- Data analysis: Regression analysis and statistical modeling.
Further exploration of these topics could include delving deeper into solving more complex systems of equations, exploring nonlinear equations, or investigating applications in specific fields mentioned above.
This extended discussion emphasizes the importance of context, clarity, and the various mathematical techniques available for solving problems involving equations. Remember that a clear problem statement is the cornerstone of successful problem-solving. Without adequate information, finding a unique solution for ‘x’ remains impossible.
Latest Posts
Latest Posts
-
Ecological Diversity Is A Measure Of The Number Of
May 10, 2025
-
Inspectors Normally Focus On Conformity To This System
May 10, 2025
-
Shaping Is Effective By Rewarding To The Desired Behavior
May 10, 2025
-
According To The Results Of The Pillbug Experiment
May 10, 2025
-
The Process Of Recording Transactions In A Journal Is Called
May 10, 2025
Related Post
Thank you for visiting our website which covers about Pr 9x 31 And Qr 43 Find X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.