Pq 2x 1 And Qr 5x 44 Find Pq
Holbox
May 08, 2025 · 4 min read
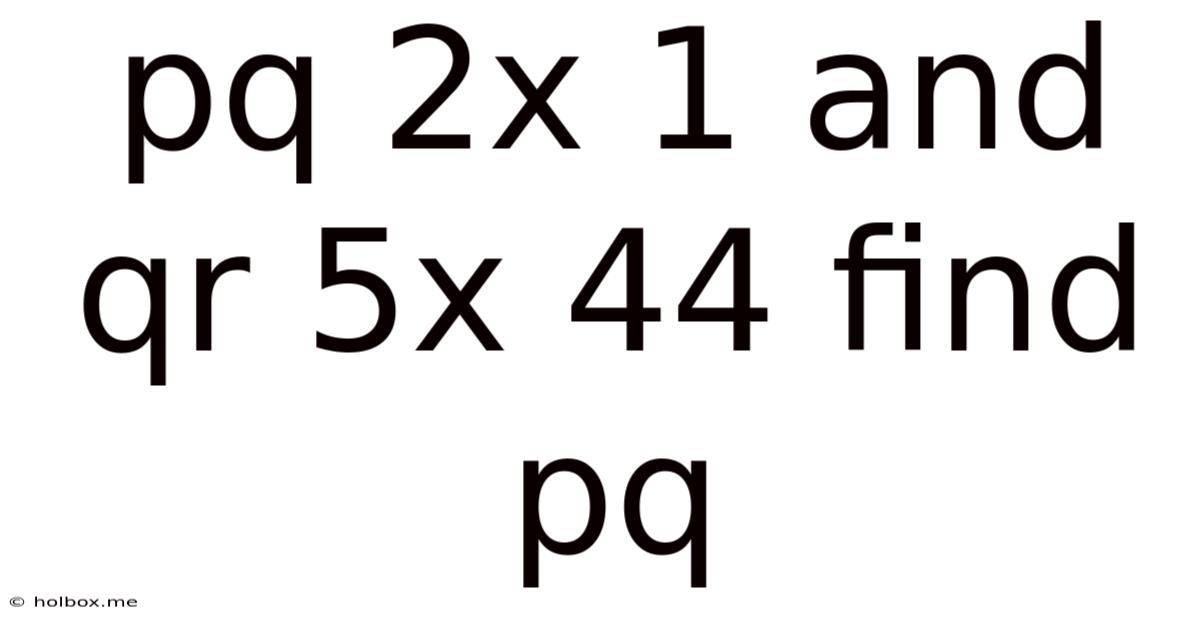
Table of Contents
- Pq 2x 1 And Qr 5x 44 Find Pq
- Table of Contents
- Solving for PQ: A Deep Dive into Vector Geometry and Analytical Solutions
- Understanding the Problem: Defining Vectors and Relationships
- Scenario 1: A and B are components of PQ
- Example: Assuming a specific relationship
- Scenario 2: A and B are Related Through Transformations
- Scenario 3: Exploring a Possible Misinterpretation
- Analytical Methods and Limitations
- Importance of Context and Additional Information
- Conclusion: The Need for Clarity and Further Data
- Latest Posts
- Related Post
Solving for PQ: A Deep Dive into Vector Geometry and Analytical Solutions
This article explores the problem of finding the vector PQ given the vectors 2x + 1 and 5x + 44, offering a comprehensive analysis of various approaches and emphasizing the importance of vector geometry in solving such problems. We will delve into the mathematical concepts, provide detailed step-by-step solutions, and discuss potential applications of these techniques.
Understanding the Problem: Defining Vectors and Relationships
Before diving into the solution, let's clarify the problem statement. We are given two vectors, let's represent them as:
- A = 2x + 1
- B = 5x + 44
We need to find the vector PQ, which implies finding the vector that connects point P to point Q. The problem, as stated, lacks sufficient information to directly solve for PQ. We need additional context or relationships between A, B, and PQ. The problem, as presented, is underdetermined. To proceed, we need to make assumptions or introduce additional constraints.
Let's explore two plausible scenarios:
Scenario 1: A and B are components of PQ
We can assume that A and B represent components of the vector PQ in a multi-dimensional space (e.g., 2D or 3D). In this case, PQ would be the vector sum of A and B.
However, this interpretation presents a challenge. Vectors A and B are expressed in terms of 'x', which is an unknown scalar. We cannot directly add them unless we know the value of 'x'. The problem remains underdetermined. To proceed, we would require additional information, such as:
- Magnitude of PQ: Knowing the length of vector PQ would provide a constraint to solve for 'x'.
- Angle or Direction of PQ: Knowledge of the angle of PQ relative to coordinate axes would impose further restrictions, allowing us to solve for 'x'.
- Relationship between A and B: Any stated relationship between A and B (e.g., they are orthogonal, parallel, or linearly dependent) could offer a solvable equation.
Example: Assuming a specific relationship
Let's hypothetically assume that A and B are parallel vectors. This means that one is a scalar multiple of the other. This can be expressed as:
A = k * B
Where 'k' is a scalar constant. Substituting the expressions for A and B, we get:
2x + 1 = k * (5x + 44)
This equation now provides a relationship between 'x' and 'k'. However, to uniquely solve for 'x', we'd need another independent equation. Without additional information, we cannot determine the value of 'x' and therefore cannot solve for PQ.
Scenario 2: A and B are Related Through Transformations
Another interpretation is that A and B represent the result of transformations on the vector PQ. For instance, A might be a projection of PQ onto a specific axis, while B is a rotation or scaling of PQ. Such transformations could be expressed using matrices. However, without specifying the exact nature of these transformations, we can't proceed.
Scenario 3: Exploring a Possible Misinterpretation
It's crucial to consider the possibility that the problem statement itself may contain an error or a misunderstanding. The notation "PQ 2x + 1" and "QR 5x + 44" suggests that these might represent lengths or magnitudes, not vectors. If this is the case, the problem becomes entirely different.
Let's assume, for the sake of argument, that these are magnitudes. Even then, the problem is underdetermined. We have two equations with three unknowns: PQ, QR, and x.
Analytical Methods and Limitations
Without additional constraints or clarifying information, finding PQ using analytical methods is impossible. The initial problem provides an insufficient number of equations to solve for the unknown variables. We need at least as many independent equations as unknowns.
The core issue lies in the lack of specific relationships between the given expressions and the vector PQ. The expressions involving 'x' introduce an additional unknown, further complicating the problem.
Importance of Context and Additional Information
The inability to solve for PQ highlights the critical role of context and additional information in mathematical problem-solving. Problems presented in isolation often lack the necessary constraints to yield a unique solution. Always carefully examine the context and identify any implicit or explicit relationships to formulate a well-defined problem that can be solved.
Conclusion: The Need for Clarity and Further Data
In conclusion, the problem of finding PQ given only 2x + 1 and 5x + 44 is unsolvable without further context or additional information. The problem is underdetermined. To solve this type of problem, we need to establish a clear relationship between the given expressions and the vector PQ. This could involve specifying the dimensions of the space, defining transformations, or providing constraints on the magnitude, direction, or relationships between the vectors involved. Further clarifying the problem statement would allow for a definitive solution. The exercise highlights the importance of precisely defining mathematical problems and providing all necessary data for accurate and meaningful results.
Latest Posts
Related Post
Thank you for visiting our website which covers about Pq 2x 1 And Qr 5x 44 Find Pq . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.