Ln X Ln X 1 Ln X 1
Holbox
May 07, 2025 · 5 min read
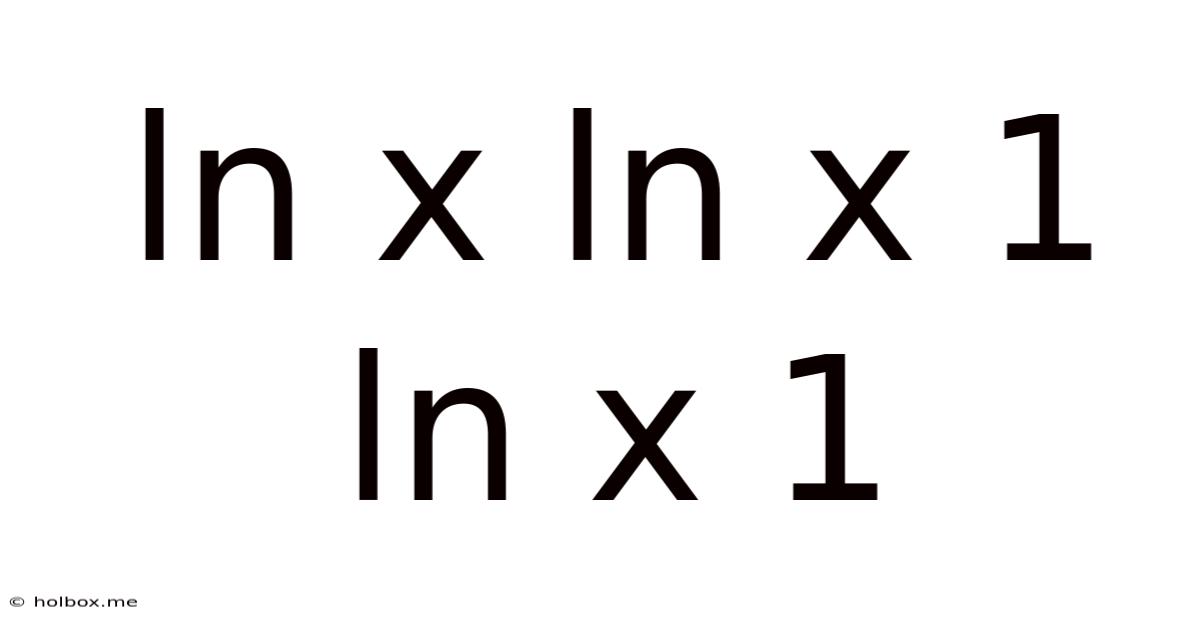
Table of Contents
- Ln X Ln X 1 Ln X 1
- Table of Contents
- Delving Deep into the Mathematical Landscape of ln(x)ln(x+1) / ln(x+1)
- Understanding the Components: Natural Logarithms and their Properties
- Simplifying the Expression: ln(x)ln(x+1) / ln(x+1)
- Analyzing the Simplified Expression: ln(x)
- Graphical Representation and Interpretation
- Limits and Asymptotic Behavior
- Applications of ln(x)
- Addressing the Original Expression's Subtlety: The Case of ln(x+1) = 0
- Further Exploration and Advanced Topics
- Conclusion
- Latest Posts
- Related Post
Delving Deep into the Mathematical Landscape of ln(x)ln(x+1) / ln(x+1)
The expression ln(x)ln(x+1) / ln(x+1) presents a fascinating challenge in mathematical analysis. At first glance, it appears deceptively simple. However, a deeper exploration reveals nuances in its behavior, domain, limits, and potential applications. This article aims to provide a comprehensive analysis of this expression, breaking down its complexities and highlighting its key characteristics.
Understanding the Components: Natural Logarithms and their Properties
Before diving into the expression itself, it's crucial to understand the fundamental properties of the natural logarithm (ln). The natural logarithm is the logarithm to the base e, where e is Euler's number (approximately 2.71828). Key properties include:
- ln(1) = 0: The natural logarithm of 1 is 0.
- ln(e) = 1: The natural logarithm of e is 1.
- ln(xy) = ln(x) + ln(y): The logarithm of a product is the sum of the logarithms.
- ln(x/y) = ln(x) - ln(y): The logarithm of a quotient is the difference of the logarithms.
- ln(xⁿ) = nln(x): The logarithm of a power is the exponent times the logarithm of the base.
- The domain of ln(x) is (0, ∞): The natural logarithm is only defined for positive real numbers.
These properties are fundamental to simplifying and analyzing the given expression.
Simplifying the Expression: ln(x)ln(x+1) / ln(x+1)
The initial expression, ln(x)ln(x+1) / ln(x+1), can be significantly simplified. Notice that ln(x+1) appears in both the numerator and the denominator. Provided that ln(x+1) ≠ 0 (which means x ≠ 0), we can cancel these terms, resulting in a much simpler expression:
ln(x)
This simplification drastically alters our analysis. Instead of dealing with a complex ratio of logarithmic functions, we now focus on the behavior of the natural logarithm of x.
Analyzing the Simplified Expression: ln(x)
The function f(x) = ln(x) is a well-studied function with several key characteristics:
- Domain: (0, ∞) – As mentioned earlier, the natural logarithm is only defined for positive values of x.
- Range: (-∞, ∞) – The natural logarithm can take on any real value.
- Behavior as x approaches 0: As x approaches 0 from the right (x → 0⁺), ln(x) approaches negative infinity (ln(x) → -∞). This signifies a vertical asymptote at x = 0.
- Behavior as x approaches infinity: As x approaches infinity (x → ∞), ln(x) also approaches infinity (ln(x) → ∞). However, it does so at a slower rate than any positive power of x.
- Derivative: The derivative of ln(x) is 1/x. This indicates that the function is always increasing for x > 0.
- Concavity: The second derivative of ln(x) is -1/x², which is always negative for x > 0. This signifies that the function is concave down.
Graphical Representation and Interpretation
A graph of y = ln(x) clearly illustrates these characteristics. The curve starts at negative infinity as x approaches 0, steadily increases, and continues to rise albeit at a decreasing rate as x approaches infinity. The graph visually demonstrates the function's asymptotic behavior and its monotonically increasing nature.
Limits and Asymptotic Behavior
Analyzing the limits of ln(x) helps to further understand its behavior at the boundaries of its domain:
- lim (x→0⁺) ln(x) = -∞: The function approaches negative infinity as x approaches 0 from the positive side. This confirms the vertical asymptote at x = 0.
- lim (x→∞) ln(x) = ∞: The function approaches infinity as x approaches infinity. However, the rate of growth is relatively slow.
Applications of ln(x)
The natural logarithm and its properties find extensive use across various fields, including:
- Calculus: ln(x) plays a crucial role in integration and differentiation. Its derivative, 1/x, is fundamental in many integration techniques.
- Physics and Engineering: Natural logarithms appear in various physical phenomena, such as radioactive decay, population growth, and heat transfer.
- Economics and Finance: Logarithmic functions are used in modeling economic growth, compound interest, and various financial models.
- Computer Science: Logarithms are fundamental in algorithm analysis, particularly in determining the time complexity of algorithms.
- Probability and Statistics: Logarithms are frequently used in statistical calculations, particularly when dealing with probabilities.
Addressing the Original Expression's Subtlety: The Case of ln(x+1) = 0
While we simplified the initial expression to ln(x), it's crucial to revisit the original expression and address a subtle point. The simplification hinged on the assumption that ln(x+1) ≠ 0. This condition requires x ≠ 0. If x were 0, the original expression would be undefined due to division by zero. Therefore, while the simplified form, ln(x), helps understand the behavior for x > 0, we must remember the original expression's limitation at x = 0.
Further Exploration and Advanced Topics
The exploration of ln(x) can be extended to more advanced topics:
- Taylor Series Expansion: The natural logarithm can be represented by its Taylor series expansion around a specific point, allowing for approximation and analysis through infinite series.
- Complex Logarithm: The concept of the natural logarithm can be extended to the complex plane, adding further complexity and richness to its mathematical properties.
- Lambert W Function: The Lambert W function, which is the inverse function of f(x) = xeˣ, has a close relationship with the natural logarithm and provides solutions to equations that cannot be solved using elementary functions.
Conclusion
The seemingly simple expression ln(x)ln(x+1) / ln(x+1) ultimately simplifies to ln(x), revealing a wealth of mathematical properties and applications. Understanding the natural logarithm, its behavior, and its limitations is crucial for navigating various fields of mathematics, science, and engineering. By exploring its domain, range, derivatives, limits, and graphical representation, we gain a comprehensive understanding of its power and versatility. Furthermore, remembering the original expression's undefined point at x = 0 reminds us of the importance of considering the context and limitations of mathematical simplifications. The journey from the initial expression to a thorough understanding of ln(x) serves as a testament to the depth and beauty inherent in mathematical analysis.
Latest Posts
Related Post
Thank you for visiting our website which covers about Ln X Ln X 1 Ln X 1 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.