If 2 X 14 Then X
Holbox
May 12, 2025 · 5 min read
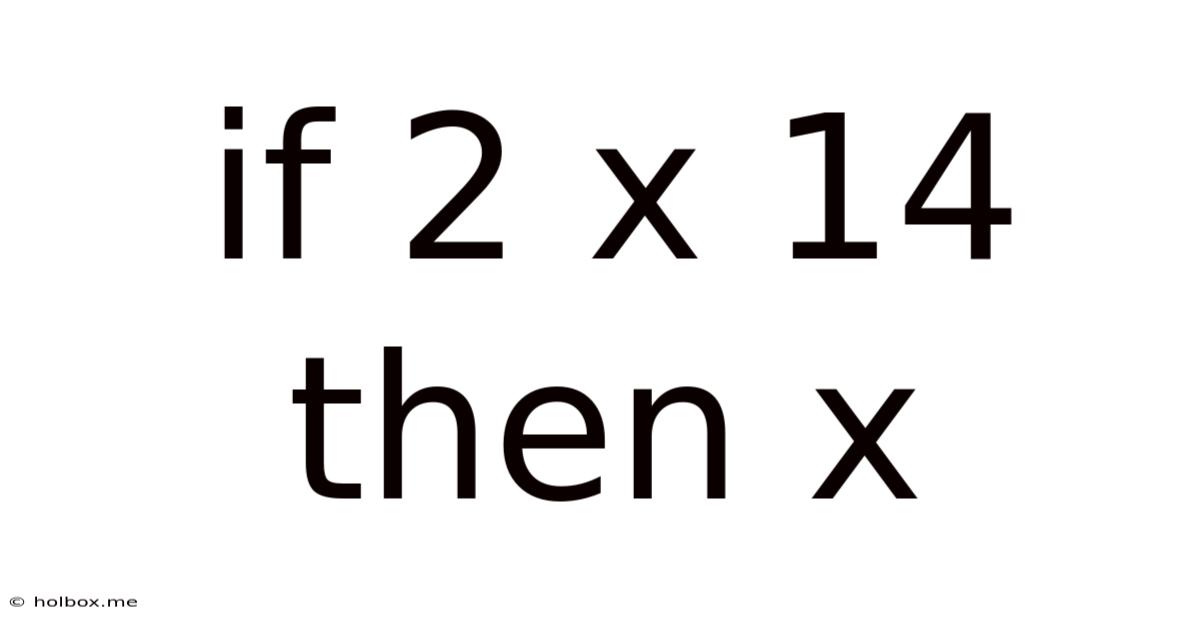
Table of Contents
- If 2 X 14 Then X
- Table of Contents
- If 2 x 14, Then x: Unveiling the Power of Algebraic Equations
- Understanding the Equation: 2 x = 14
- Defining the Terms
- Solving for x: Methods and Techniques
- 1. The Division Method
- 2. The Subtraction Method (Less Direct, but Illustrative)
- Verification and Proof
- Expanding the Concept: Beyond Simple Equations
- 1. Equations with Multiple Variables
- 2. Equations with Exponents
- 3. Equations with Fractions
- 4. Equations with Roots
- Real-World Applications
- Conclusion: The Power of Simple Equations
- Latest Posts
- Latest Posts
- Related Post
If 2 x 14, Then x: Unveiling the Power of Algebraic Equations
Mathematics, at its core, is a language of relationships. It allows us to describe and understand the intricate connections between quantities and variables. A seemingly simple equation like "2 x 14" immediately presents a challenge: to find the value of 'x' that satisfies this relationship. This seemingly elementary problem serves as a springboard to explore fundamental algebraic concepts, problem-solving techniques, and the beauty of mathematical logic.
Understanding the Equation: 2 x = 14
The equation "2 x = 14" represents a fundamental concept in algebra: solving for an unknown variable. Here, 'x' is our unknown, and the equation states that twice the value of 'x' equals 14. Our goal is to isolate 'x' to determine its numerical value.
Defining the Terms
Before delving into the solution, let's define the key terms:
- Variable: A variable, represented by a letter (like 'x' in this case), is a symbol that represents an unknown quantity.
- Coefficient: The number preceding a variable (in this case, '2') is called the coefficient. It indicates the multiplicative factor of the variable.
- Equation: An equation is a mathematical statement indicating that two expressions are equal. The equals sign (=) separates the two expressions.
- Solving the equation: This refers to the process of finding the value of the unknown variable that makes the equation true.
Solving for x: Methods and Techniques
There are several methods to solve for 'x' in the equation 2x = 14. Let's explore two fundamental approaches:
1. The Division Method
This is the most straightforward method. Since 'x' is multiplied by 2, we perform the inverse operation – division – to isolate 'x'. We divide both sides of the equation by 2:
2x = 14
2x / 2 = 14 / 2
x = 7
Therefore, the solution to the equation 2x = 14 is x = 7. This means that if we substitute 7 for 'x' in the original equation, we get a true statement: 2 * 7 = 14.
2. The Subtraction Method (Less Direct, but Illustrative)
While less direct for this specific equation, the subtraction method demonstrates a more generalizable approach applicable to more complex equations. This involves manipulating the equation to isolate 'x'. While not ideal here, it highlights important algebraic principles.
Although not directly applicable in this simple equation, a related equation like 2x + 5 = 19 requires a multi-step approach, emphasizing the importance of this method.
Imagine, for example, the equation 2x + 5 = 19. To solve, we follow these steps:
-
Subtract 5 from both sides: This isolates the term with 'x'.
2x + 5 - 5 = 19 - 52x = 14 -
Divide both sides by 2: This isolates 'x'.
2x / 2 = 14 / 2x = 7
This highlights that even seemingly simple equations can form the building blocks for understanding more complex algebraic problems.
Verification and Proof
To ensure our solution is correct, we can verify it by substituting the value of 'x' back into the original equation:
2 * 7 = 14
The equation holds true, confirming that our solution, x = 7, is accurate. This verification step is crucial in all mathematical problem-solving, providing confidence in the accuracy of the solution.
Expanding the Concept: Beyond Simple Equations
While the equation 2x = 14 provides a foundational understanding of algebraic problem-solving, let's expand this concept to explore more complex scenarios:
1. Equations with Multiple Variables
Consider an equation like 2x + 3y = 17. Solving this requires additional information, such as another equation involving 'x' and 'y' (a system of equations). This introduces the concept of simultaneous equations, where we use various methods like substitution or elimination to find the values of 'x' and 'y'.
2. Equations with Exponents
Equations involving exponents, such as 2x² = 18, introduce a different level of complexity. Solving such quadratic equations often involves techniques like factoring, completing the square, or using the quadratic formula.
3. Equations with Fractions
Equations involving fractions, like (x/2) + 3 = 5, require specific steps to clear the fraction. This often involves multiplying both sides of the equation by the denominator to eliminate the fraction.
4. Equations with Roots
Equations with square roots or other roots, like √x + 2 = 5, necessitate specific methods to isolate the variable. Squaring both sides (carefully considering potential extraneous solutions) is a common technique.
Real-World Applications
The ability to solve simple algebraic equations like 2x = 14 extends far beyond the realm of theoretical mathematics. It forms the basis for problem-solving in numerous real-world applications, including:
- Physics: Calculating velocities, accelerations, and forces.
- Engineering: Determining dimensions, stresses, and strains in structures.
- Finance: Calculating interest, compound growth, and loan repayments.
- Chemistry: Determining the quantities of reactants and products in chemical reactions.
- Computer Science: Developing algorithms and solving computational problems.
Conclusion: The Power of Simple Equations
The seemingly simple equation 2x = 14 provides a powerful entry point into the world of algebra. Mastering the techniques to solve such equations is essential for tackling more complex mathematical problems and applying mathematical principles to real-world scenarios. The ability to manipulate equations, isolate variables, and verify solutions is not only a mathematical skill but a vital tool for critical thinking and problem-solving in various fields. By understanding the fundamentals, we unlock a gateway to a deeper appreciation of the beauty and power of mathematics. Remember the power of verification; always check your answer! Practice makes perfect, so continue solving equations to solidify your understanding and build confidence in your mathematical abilities. The journey from simple equations to complex mathematical models begins with mastering the basics – and mastering the basics starts here.
Latest Posts
Latest Posts
-
214 8 Lbs To Stone And Pounds
May 21, 2025
-
What Is 122 Cm In Inches
May 21, 2025
-
1 95 Kilos In Pounds And Ounces
May 21, 2025
-
171 Cm To Feet And Inches
May 21, 2025
-
How Many Stone Is 85 Kilos
May 21, 2025
Related Post
Thank you for visiting our website which covers about If 2 X 14 Then X . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.