Four More Than A Number Is More Than 13
Holbox
May 09, 2025 · 5 min read
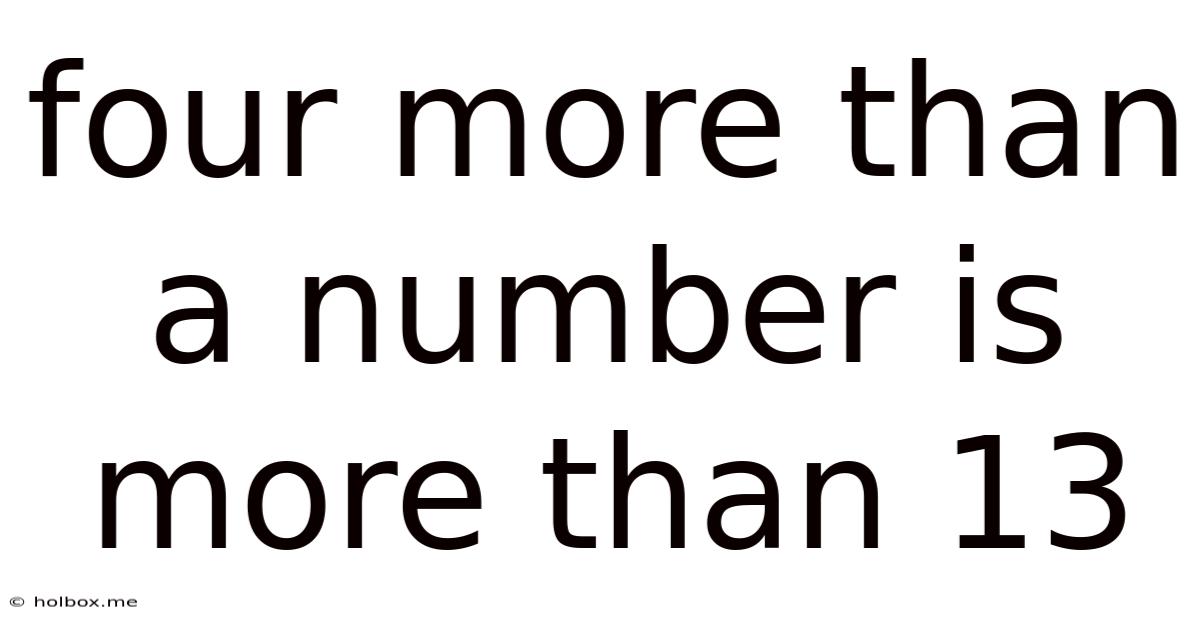
Table of Contents
- Four More Than A Number Is More Than 13
- Table of Contents
- Four More Than a Number is More Than 13: A Deep Dive into Inequalities
- Understanding the Problem: From Words to Algebra
- Solving the Inequality: Unveiling the Solution Set
- Visualizing the Solution: Number Lines and Graphs
- Expanding the Concept: Variations and Extensions
- 1. "Four more than a number is at least 13"
- 2. "Four more than twice a number is less than 13"
- 3. Compound Inequalities: Combining Multiple Conditions
- Real-World Applications: Inequalities in Everyday Life
- Advanced Concepts: Absolute Value Inequalities
- Strategies for Problem Solving: A Step-by-Step Approach
- Conclusion: Mastering Inequalities for Mathematical Success
- Latest Posts
- Latest Posts
- Related Post
Four More Than a Number is More Than 13: A Deep Dive into Inequalities
This seemingly simple statement, "four more than a number is more than 13," hides a wealth of mathematical concepts and problem-solving strategies. This article will explore this inequality in detail, examining its translation into algebraic form, various methods for solving it, and its real-world applications. We'll also delve into related concepts and discuss how to approach similar problems effectively.
Understanding the Problem: From Words to Algebra
The core of this problem lies in translating the verbal description into a mathematical inequality. Let's break down the phrase step by step:
- "a number": This represents an unknown value, typically represented by a variable, often 'x'.
- "four more than a number": This translates to
x + 4. We are adding 4 to our unknown number. - "is more than 13": This indicates an inequality, meaning the expression
x + 4is greater than 13. This is expressed asx + 4 > 13.
Therefore, the complete algebraic representation of the statement "four more than a number is more than 13" is: x + 4 > 13
Solving the Inequality: Unveiling the Solution Set
Solving this inequality involves isolating the variable 'x' to determine the range of values that satisfy the condition. We achieve this using inverse operations, remembering that the inequality sign flips if we multiply or divide by a negative number.
- Subtract 4 from both sides: This step eliminates the constant term on the left side, leaving us with:
x + 4 - 4 > 13 - 4which simplifies to:x > 9
This solution tells us that any number greater than 9 satisfies the original inequality. This is not a single solution, but rather a set of solutions, an infinite number of possibilities.
Visualizing the Solution: Number Lines and Graphs
Representing the solution set graphically using a number line provides a clear visual understanding. We would draw a number line, mark 9, and then shade the region to the right of 9. A hollow circle (or parenthesis) at 9 indicates that 9 itself is not included in the solution set (because the inequality is strictly greater than).
This visual representation is crucial for understanding the range of values that solve the inequality. It's a powerful tool, particularly when dealing with more complex inequalities.
Expanding the Concept: Variations and Extensions
The fundamental principle of translating word problems into algebraic expressions applies to a multitude of scenarios. Let's consider some variations:
1. "Four more than a number is at least 13"
This subtly changes the inequality. "At least 13" means the expression is greater than or equal to 13. The inequality becomes:
x + 4 ≥ 13
Solving this yields: x ≥ 9. The only difference is that now 9 is included in the solution set, represented by a filled circle (or bracket) on the number line.
2. "Four more than twice a number is less than 13"
This introduces another layer of complexity. The translation is:
2x + 4 < 13
Solving this requires multiple steps:
- Subtract 4 from both sides:
2x < 9 - Divide both sides by 2:
x < 4.5
The solution set includes all numbers less than 4.5.
3. Compound Inequalities: Combining Multiple Conditions
We can extend this further by combining multiple inequalities. For example:
"Four more than a number is more than 13, but less than 20"
This translates to a compound inequality:
13 < x + 4 < 20
To solve this, we subtract 4 from all parts of the inequality:
9 < x < 16
The solution set includes all numbers between 9 and 16 (excluding 9 and 16 themselves).
Real-World Applications: Inequalities in Everyday Life
While seemingly abstract, inequalities have numerous real-world applications:
-
Budgeting: If you have $20 and need to buy groceries, you might want to spend less than that. This could be expressed as an inequality involving the cost of groceries.
-
Speed Limits: Speed limits are essentially inequalities. You must drive at a speed less than or equal to a certain value.
-
Temperature Ranges: Weather forecasts often provide temperature ranges, representing inequalities.
-
Manufacturing Tolerances: In manufacturing, parts must often fall within a certain size range, expressed using inequalities.
-
Optimization Problems: Many optimization problems in fields like engineering and economics involve finding the best solution within a set of constraints, often expressed as inequalities.
Advanced Concepts: Absolute Value Inequalities
Another important extension involves absolute value inequalities. For example:
|x + 4| > 13
This means the distance between x + 4 and 0 is greater than 13. This translates into two separate inequalities:
x + 4 > 13 or x + 4 < -13
Solving each separately gives:
x > 9 or x < -17
The solution set is the union of these two ranges.
Strategies for Problem Solving: A Step-by-Step Approach
Successfully tackling word problems involving inequalities requires a systematic approach:
-
Careful Reading: Understand the problem statement completely.
-
Define Variables: Assign variables to represent unknown quantities.
-
Translate to Algebra: Convert the word problem into a mathematical inequality.
-
Solve the Inequality: Use algebraic techniques to isolate the variable.
-
Interpret the Solution: Understand the meaning of the solution in the context of the problem.
-
Check your Answer: Substitute a value from the solution set back into the original inequality to verify it satisfies the condition.
Conclusion: Mastering Inequalities for Mathematical Success
Understanding and solving inequalities is a fundamental skill in mathematics with far-reaching applications. By mastering the techniques outlined in this article, you can confidently tackle a wide range of problems involving inequalities, enhancing your problem-solving skills and expanding your mathematical knowledge. Remember to practice regularly, exploring various problem types and applying the systematic approach to solidify your understanding. The journey from a simple statement like "four more than a number is more than 13" to a comprehensive grasp of inequalities is a rewarding one, unlocking a deeper understanding of the mathematical world around us.
Latest Posts
Latest Posts
-
What Is 186 Cm In Ft
May 20, 2025
-
83 10 Kg In Stone And Pounds
May 20, 2025
-
How Many Hours Are In 240 Minutes
May 20, 2025
-
How Many Hours In 20 Days
May 20, 2025
-
What Is 185 Pounds In Stone
May 20, 2025
Related Post
Thank you for visiting our website which covers about Four More Than A Number Is More Than 13 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.