Find The Following Integral Given That
Holbox
Apr 05, 2025 · 5 min read
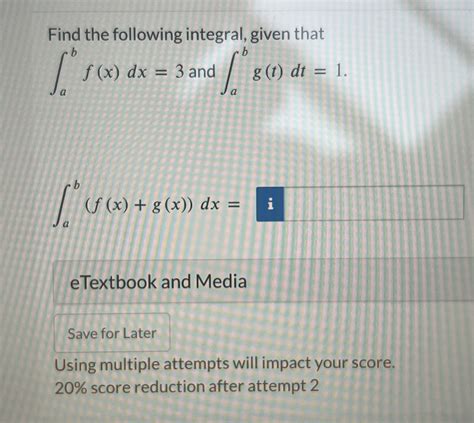
Table of Contents
- Find The Following Integral Given That
- Table of Contents
- Finding the Integral: A Comprehensive Guide with Examples
- Understanding the Basics: Indefinite Integrals
- Mastering Integration Techniques
- 1. u-Substitution (Integration by Substitution)
- 2. Integration by Parts
- 3. Partial Fraction Decomposition
- 4. Trigonometric Integrals
- 5. Dealing with Definite Integrals
- Advanced Integration Techniques
- Tips and Strategies for Successful Integration
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Finding the Integral: A Comprehensive Guide with Examples
Finding integrals, also known as antiderivatives, is a fundamental concept in calculus. This process reverses the operation of differentiation, allowing us to determine the original function from its derivative. While some integrals are straightforward, many require specific techniques and strategies to solve. This comprehensive guide will explore various methods for finding integrals, illustrating each with detailed examples. We'll cover basic integration rules, techniques like substitution, integration by parts, and partial fraction decomposition, along with handling definite and indefinite integrals.
Understanding the Basics: Indefinite Integrals
An indefinite integral represents the general antiderivative of a function. It's denoted by the integral symbol ∫, followed by the function and dx, indicating integration with respect to x. The result always includes an arbitrary constant, C, because the derivative of a constant is zero.
Example:
Find the indefinite integral of f(x) = 2x.
The power rule of integration states: ∫xⁿ dx = (xⁿ⁺¹)/(n+1) + C
Applying this rule:
∫2x dx = 2∫x¹ dx = 2 * (x¹⁺¹)/(1+1) + C = x² + C
Therefore, the indefinite integral of 2x is x² + C. The constant 'C' accounts for any possible constant that could have been part of the original function before differentiation.
Mastering Integration Techniques
Several techniques are crucial for tackling more complex integrals. Let's explore some of the most important ones:
1. u-Substitution (Integration by Substitution)
This technique is incredibly useful when dealing with composite functions. It involves substituting a part of the integrand with a new variable, u, to simplify the integral.
Example:
Find the integral of ∫x(x²+1)³ dx.
- Choose u: Let u = x² + 1.
- Find du: Differentiating u with respect to x, we get du = 2x dx. This means x dx = du/2.
- Substitute: Replace (x² + 1) with u and x dx with du/2 in the integral: ∫u³ (du/2) = (1/2)∫u³ du
- Integrate: Apply the power rule: (1/2) * (u⁴/4) + C = u⁴/8 + C
- Substitute back: Replace u with x² + 1: (x² + 1)⁴/8 + C
Therefore, the integral of x(x² + 1)³ dx is (x² + 1)⁴/8 + C.
2. Integration by Parts
Integration by parts is based on the product rule for differentiation. It's particularly helpful when integrating products of functions. The formula is:
∫u dv = uv - ∫v du
The key is choosing appropriate u and dv to simplify the integral. The acronym LIATE (Logarithmic, Inverse trigonometric, Algebraic, Trigonometric, Exponential) can help in selecting u.
Example:
Find the integral of ∫x * eˣ dx.
- Choose u and dv: Let u = x and dv = eˣ dx.
- Find du and v: Differentiating u, we get du = dx. Integrating dv, we get v = eˣ.
- Apply the formula: ∫x * eˣ dx = x * eˣ - ∫eˣ dx
- Integrate: ∫eˣ dx = eˣ + C
- Combine: x * eˣ - eˣ + C
Therefore, the integral of x * eˣ dx is x * eˣ - eˣ + C.
3. Partial Fraction Decomposition
This technique is useful for integrating rational functions (fractions where the numerator and denominator are polynomials). It involves breaking down the rational function into simpler fractions that are easier to integrate.
Example:
Find the integral of ∫(2x + 3)/(x² - 1) dx.
- Factor the denominator: x² - 1 = (x - 1)(x + 1)
- Decompose into partial fractions: (2x + 3)/(x² - 1) = A/(x - 1) + B/(x + 1)
- Solve for A and B: Multiply both sides by (x - 1)(x + 1) and solve the resulting equation for A and B (using methods like equating coefficients or substituting values of x). You'll find A = 5/2 and B = -1/2.
- Integrate: ∫(5/2)/(x - 1) dx + ∫(-1/2)/(x + 1) dx = (5/2)ln|x - 1| - (1/2)ln|x + 1| + C
Therefore, the integral of (2x + 3)/(x² - 1) dx is (5/2)ln|x - 1| - (1/2)ln|x + 1| + C
4. Trigonometric Integrals
Integrating trigonometric functions often requires trigonometric identities and substitutions.
Example:
Find the integral of ∫sin²x dx.
Using the identity sin²x = (1 - cos2x)/2:
∫sin²x dx = ∫(1 - cos2x)/2 dx = (1/2)∫(1 - cos2x) dx = (1/2)(x - (1/2)sin2x) + C = x/2 - (1/4)sin2x + C
5. Dealing with Definite Integrals
A definite integral calculates the area under a curve between two specified limits. It's denoted by ∫ᵇₐ f(x) dx, where a and b are the lower and upper limits of integration. The process involves finding the indefinite integral and then evaluating it at the limits.
Example:
Evaluate the definite integral ∫₂¹ x² dx.
- Find the indefinite integral: ∫x² dx = x³/3 + C
- Evaluate at the limits: [(2)³/3 + C] - [(1)³/3 + C] = 8/3 - 1/3 = 7/3.
The value of the definite integral is 7/3. Note that the constant C cancels out when evaluating definite integrals.
Advanced Integration Techniques
For particularly challenging integrals, more advanced techniques may be necessary, including:
- Trigonometric Substitution: Used when the integrand contains expressions like √(a² - x²), √(a² + x²), or √(x² - a²). Appropriate trigonometric substitutions simplify these expressions.
- Improper Integrals: These integrals involve infinite limits or integrands with discontinuities within the integration interval. They require careful handling of limits.
- Numerical Integration: When analytical methods fail, numerical techniques like the Trapezoidal Rule or Simpson's Rule provide approximate solutions.
Tips and Strategies for Successful Integration
- Practice Regularly: The more you practice, the better you'll become at recognizing patterns and selecting the appropriate techniques.
- Master Basic Rules: A solid understanding of the power rule, constant multiple rule, sum/difference rule, and basic trigonometric integrals is essential.
- Simplify Before Integrating: Often, algebraic simplification can greatly reduce the complexity of an integral.
- Check Your Work: Differentiate your result to ensure it matches the original integrand.
- Use Technology Wisely: Computer algebra systems (CAS) can help verify solutions and provide hints for difficult integrals, but understand the underlying methods.
Conclusion
Finding integrals is a vital skill in calculus and has applications across numerous fields. This guide provides a solid foundation, covering fundamental techniques and strategies for tackling a wide range of integrals. Remember to practice consistently and explore additional resources to enhance your understanding and proficiency. With dedication and practice, you'll master this essential mathematical concept and apply it to solve complex problems.
Latest Posts
Latest Posts
-
Which Of The Following Statements Are True Regarding Corporations
Apr 09, 2025
-
Businesses Must Monitor The Factors In Their Environment To
Apr 09, 2025
-
Is Garlic Powder A Pure Substance Or Mixture
Apr 09, 2025
-
You Ring Up An Item For A Customer
Apr 09, 2025
-
Save The Current Workbook To The Workshops Folder
Apr 09, 2025
Related Post
Thank you for visiting our website which covers about Find The Following Integral Given That . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.