Evaluate The Line Integral Along The Curve C
Holbox
Mar 27, 2025 · 6 min read
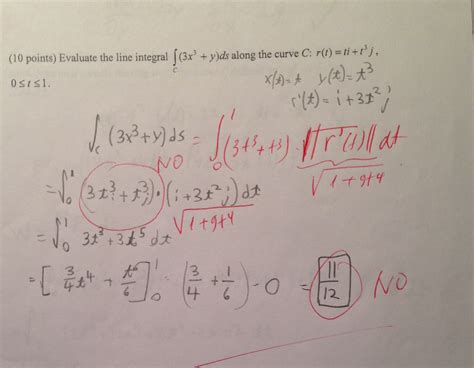
Table of Contents
- Evaluate The Line Integral Along The Curve C
- Table of Contents
- Evaluating Line Integrals Along a Curve C: A Comprehensive Guide
- Understanding Line Integrals
- Evaluating Line Integrals: Scalar Fields
- Evaluating Line Integrals: Vector Fields
- Special Cases and Considerations
- Applications of Line Integrals
- Advanced Techniques and Theorems
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Evaluating Line Integrals Along a Curve C: A Comprehensive Guide
Line integrals are a fundamental concept in vector calculus, extending the idea of a definite integral to curves in space. They find widespread applications in physics and engineering, modeling concepts like work done by a force field, circulation of a fluid, and flux across a curve. This article provides a comprehensive guide to evaluating line integrals along a curve C, covering various methods and scenarios.
Understanding Line Integrals
A line integral calculates the accumulation of a function along a curve. Unlike single-variable integrals that operate over intervals, line integrals integrate over paths. The function being integrated can be a scalar field (a function assigning a scalar value to each point in space) or a vector field (a function assigning a vector to each point).
The general form of a line integral is expressed as:
∫<sub>C</sub> f(x, y) ds (for scalar fields)
or
∫<sub>C</sub> F • dr (for vector fields)
where:
- C represents the curve along which the integration occurs.
- f(x, y) is the scalar function (in 2D; extend to f(x, y, z) in 3D).
- F is the vector field.
- ds represents an infinitesimal arc length along the curve.
- dr is an infinitesimal displacement vector along the curve.
- • denotes the dot product.
Evaluating Line Integrals: Scalar Fields
For line integrals of scalar fields, the process involves parameterizing the curve and then integrating over the parameter.
1. Parameterization:
The first step is to parameterize the curve C. This involves expressing x and y (and z in 3D) in terms of a single parameter, usually denoted by 't'. For example, a straight line segment from (x₁, y₁) to (x₂, y₂) can be parameterized as:
x = x₁ + t(x₂ - x₁) y = y₁ + t(y₂ - y₁)
where 0 ≤ t ≤ 1. More complex curves might require trigonometric functions or other techniques.
2. Calculating ds:
Next, we need to find ds, the infinitesimal arc length. This is given by:
ds = √[(dx/dt)² + (dy/dt)²] dt (in 2D)
or
ds = √[(dx/dt)² + (dy/dt)² + (dz/dt)²] dt (in 3D)
3. Integration:
Finally, substitute the parameterized x, y (and z), and ds into the line integral and integrate with respect to t over the appropriate interval.
Example: Evaluate ∫<sub>C</sub> (x + y) ds, where C is the line segment from (0, 0) to (1, 1).
- Parameterization: x = t, y = t, 0 ≤ t ≤ 1
- ds: ds = √[(dx/dt)² + (dy/dt)²] dt = √(1² + 1²) dt = √2 dt
- Integration: ∫<sub>0</sub><sup>1</sup> (t + t)√2 dt = √2 ∫<sub>0</sub><sup>1</sup> 2t dt = √2 [t²]<sub>0</sub><sup>1</sup> = √2
Evaluating Line Integrals: Vector Fields
Line integrals of vector fields are significantly different, involving the dot product of the vector field and the tangent vector to the curve.
1. Parameterization (Again):
Similar to scalar fields, we need to parameterize the curve C.
2. Calculating dr:
The infinitesimal displacement vector dr is given by:
dr = (dx/dt) i + (dy/dt) j + (dz/dt) k dt (in 3D)
3. The Dot Product:
The key step here is taking the dot product of the vector field F and dr. This projects the vector field onto the tangent vector of the curve, providing the component of the field acting along the curve.
4. Integration:
Finally, substitute the parameterized x, y (and z), and the dot product into the integral and integrate with respect to t.
Example: Evaluate ∫<sub>C</sub> F • dr, where F = xi + yj and C is the parabola y = x², from (0, 0) to (1, 1).
- Parameterization: x = t, y = t², 0 ≤ t ≤ 1
- dr:** dr = i + 2tj dt
- F: F = ti + t²j
- Dot Product: F • dr = (ti + t²j) • (i + 2tj) dt = (t + 2t³) dt
- Integration: ∫<sub>0</sub><sup>1</sup> (t + 2t³) dt = [t²/2 + t⁴/2]<sub>0</sub><sup>1</sup> = 1
Special Cases and Considerations
-
Closed Curves: If the curve C is closed (starts and ends at the same point), the line integral is often denoted as ∮<sub>C</sub>. These integrals are crucial in calculating circulation and flux. Green's theorem relates a line integral around a closed curve to a double integral over the enclosed region.
-
Conservative Vector Fields: If the vector field F is conservative (meaning it's the gradient of a scalar potential function), the line integral is path-independent. This significantly simplifies the calculation, as the integral only depends on the endpoints of the curve.
-
Piecewise Smooth Curves: For curves that are not smooth everywhere (e.g., they have sharp corners), the line integral is evaluated as a sum of integrals over each smooth segment.
-
Multiple Variables and Higher Dimensions: The principles extend to functions of more than two or three variables and higher-dimensional curves. However, the complexity increases with dimensionality.
Applications of Line Integrals
Line integrals have numerous applications across various fields:
-
Physics: Calculating the work done by a force field along a path. The force field acts as the vector field, and the line integral provides the total work.
-
Fluid Dynamics: Computing the circulation of a fluid flow around a curve. Circulation indicates the tendency of the fluid to rotate.
-
Electromagnetism: Determining the electromotive force (EMF) induced in a wire loop moving through a magnetic field. Faraday's law utilizes line integrals.
-
Engineering: Analyzing the stress and strain along structural components.
Advanced Techniques and Theorems
Several theorems significantly simplify the evaluation of line integrals under certain conditions:
-
Green's Theorem: Relates a line integral around a simple closed curve to a double integral over the region enclosed by the curve. Useful for converting line integrals into double integrals, often simpler to evaluate.
-
Stokes' Theorem: Generalizes Green's theorem to three dimensions, relating a line integral around a closed curve to a surface integral over a surface bounded by the curve.
-
The Fundamental Theorem for Line Integrals: States that for conservative vector fields, the line integral depends only on the endpoints of the curve.
Conclusion
Evaluating line integrals requires careful understanding of parameterization, differentiation, and integration techniques. The choice of method depends heavily on the nature of the curve and the function being integrated. Mastering line integrals is essential for anyone pursuing advanced studies in calculus, physics, and engineering. By carefully considering the type of field and the curve, and by leveraging appropriate theorems, complex problems can be tackled effectively. Remember to practice a variety of examples to solidify your understanding and build your problem-solving skills. The more you work with line integrals, the more intuitive and straightforward the process will become.
Latest Posts
Latest Posts
-
Varcarolis Foundations Of Psychiatric Mental Health Nursing A Clinical Approach
Mar 31, 2025
-
For Accounts Receivable The Longer An Account Is Outstanding
Mar 31, 2025
-
Which Of The Following Is Not A Data Cleansing Activity
Mar 31, 2025
-
Choose The Correct Order Of Steps In The Production Process
Mar 31, 2025
-
Theoretical Basis For Nursing 6th Edition
Mar 31, 2025
Related Post
Thank you for visiting our website which covers about Evaluate The Line Integral Along The Curve C . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
