Evaluate Each Of The Following Expressions Given That
Holbox
Mar 27, 2025 · 5 min read
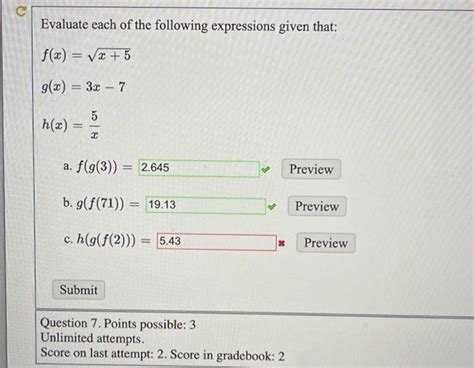
Table of Contents
Evaluating Mathematical Expressions: A Comprehensive Guide
Evaluating mathematical expressions is a fundamental skill in mathematics and programming. It involves substituting given values for variables and performing the calculations according to the order of operations (often remembered by the acronym PEMDAS/BODMAS). This article will delve into the process of evaluating various expressions, covering different levels of complexity and highlighting common pitfalls to avoid. We'll explore numerous examples, providing a thorough understanding of the techniques involved.
Understanding the Order of Operations (PEMDAS/BODMAS)
Before we begin evaluating expressions, it's crucial to understand the order of operations. PEMDAS and BODMAS are mnemonics that represent the same order:
- Parentheses (or Brackets): Calculations within parentheses/brackets are performed first.
- Exponents (or Orders): Exponents (powers) are evaluated next.
- Multiplication and Division: These operations are performed from left to right.
- Addition and Subtraction: These operations are also performed from left to right.
Remember, multiplication and division have equal precedence, as do addition and subtraction. When they appear together in an expression, we work from left to right.
Example 1: Simple Arithmetic Expressions
Let's start with some simple expressions:
-
10 + 5 * 2Following PEMDAS/BODMAS, we first perform the multiplication:
5 * 2 = 10. Then, we perform the addition:10 + 10 = 20. Therefore, the value of the expression is 20. -
20 / 4 - 2 * 3Here, we perform multiplication and division from left to right. First,
20 / 4 = 5, then2 * 3 = 6. Finally,5 - 6 = -1. The result is -1. -
(15 - 5) / 2 + 4Parentheses take precedence. First,
15 - 5 = 10. Then,10 / 2 = 5. Finally,5 + 4 = 9. The answer is 9.
Example 2: Expressions with Exponents
Exponents add another layer of complexity:
-
2³ + 4 * 2First, we evaluate the exponent:
2³ = 8. Then,4 * 2 = 8. Finally,8 + 8 = 16. The result is 16. -
(3 + 2)² - 10The parentheses are evaluated first:
3 + 2 = 5. Then,5² = 25. Finally,25 - 10 = 15. The answer is 15. -
5² * 2 - 10 / 5We evaluate the exponent first:
5² = 25. Then,25 * 2 = 50. Next,10 / 5 = 2. Finally,50 - 2 = 48. The result is 48.
Example 3: Expressions with Multiple Operations and Parentheses
Let's tackle more complex expressions:
-
100 / (2 + 3)² - 5 * 2 + 1First, we evaluate the parentheses:
2 + 3 = 5. Then,5² = 25. Next,100 / 25 = 4. Then,5 * 2 = 10. Finally,4 - 10 + 1 = -5. The answer is -5. -
[(12 - 4) / 2]³ + 7 * 3 - 1We work from the innermost parentheses outward:
12 - 4 = 8. Then,8 / 2 = 4. Then,4³ = 64. Next,7 * 3 = 21. Finally,64 + 21 - 1 = 84. The answer is 84. -
(5 + 2 * 3) / (1 + 2²) * 4 - 1Parentheses first: inside the first parentheses, multiplication before addition:
2 * 3 = 6, then5 + 6 = 11. Inside the second parentheses, exponent first:2² = 4, then1 + 4 = 5. Then,11 / 5 = 2.2. Then,2.2 * 4 = 8.8. Finally,8.8 - 1 = 7.8. The answer is 7.8.
Example 4: Expressions with Negative Numbers
Working with negative numbers requires careful attention to signs:
-
-5 + 10 - (-3)Remember that subtracting a negative is the same as adding a positive:
-5 + 10 + 3 = 8. The answer is 8. -
(-2)² - 4 * (-1)Squaring a negative number results in a positive number:
(-2)² = 4. Then,4 * (-1) = -4. Finally,4 - (-4) = 8. The answer is 8. -
-10 / 2 + 5 * (-2)Division and multiplication from left to right:
-10 / 2 = -5, then5 * (-2) = -10. Finally,-5 + (-10) = -15. The answer is -15.
Example 5: Expressions with Variables
When variables are involved, we substitute the given values:
Let's say: a = 5, b = 2, c = -3
-
a + b * cSubstituting the values:
5 + 2 * (-3) = 5 + (-6) = -1. The answer is -1. -
(a + b)² / cSubstituting the values:
(5 + 2)² / (-3) = 7² / (-3) = 49 / (-3) = -16.333.... The answer is -16.333... -
a² - b³ + cSubstituting the values:
5² - 2³ + (-3) = 25 - 8 - 3 = 14. The answer is 14.
Common Mistakes to Avoid
- Ignoring the order of operations: This is the most frequent error. Always follow PEMDAS/BODMAS carefully.
- Incorrect handling of negative numbers: Pay close attention to signs, especially when squaring or multiplying negative numbers.
- Parentheses errors: Ensure that parentheses are correctly placed and balanced. Missing or misplaced parentheses can drastically alter the result.
- Errors in decimal calculations: Double-check your calculations, particularly when dealing with decimal numbers.
Conclusion:
Evaluating mathematical expressions is a fundamental skill that requires a thorough understanding of the order of operations and careful attention to detail. By consistently following PEMDAS/BODMAS and practicing with various examples, you can master this crucial skill and improve your problem-solving abilities in mathematics and beyond. Remember to break down complex expressions into smaller, manageable parts, and always double-check your work to avoid common mistakes. With consistent practice, you will build confidence and accuracy in evaluating even the most intricate expressions. This comprehensive guide should equip you with the knowledge and practice needed to confidently tackle a wide variety of mathematical expressions. Remember, accuracy and precision are paramount in mathematics, so always take your time and work methodically.
Latest Posts
Latest Posts
-
Job Order Production Is Also Known As
Mar 30, 2025
-
A Firm Pursuing A Best Cost Provider Strategy
Mar 30, 2025
-
Match Each Respiratory Volume To Its Definition
Mar 30, 2025
-
What Stage Of Cell Division Does This Image Show
Mar 30, 2025
-
Hardcover Discovering Music Third Edition Textbook
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Evaluate Each Of The Following Expressions Given That . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
