Conversion Factors And Problem Solving Lab 2 Report Sheet Answers
Holbox
Mar 26, 2025 · 5 min read
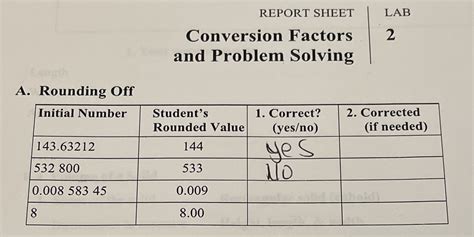
Table of Contents
- Conversion Factors And Problem Solving Lab 2 Report Sheet Answers
- Table of Contents
- Conversion Factors and Problem Solving Lab 2: A Comprehensive Guide
- Understanding Conversion Factors
- Common Conversion Factors
- Problem Solving Strategies using Conversion Factors
- Lab 2 Report Sheet Answers: Common Challenges and Solutions
- Challenge 1: Incorrect Unit Cancellation
- Challenge 2: Multiple Conversion Factors
- Challenge 3: Significant Figures and Rounding
- Challenge 4: Understanding Scientific Notation
- Challenge 5: Interpreting Experimental Data
- Example Problems and Solutions
- Advanced Topics and Considerations
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
Conversion Factors and Problem Solving Lab 2: A Comprehensive Guide
This comprehensive guide delves into the intricacies of conversion factors and their application in problem-solving, specifically focusing on the common challenges encountered in Lab 2 reports. We'll explore various aspects, providing detailed explanations, example problems, and strategies to enhance your understanding and improve your report writing.
Understanding Conversion Factors
A conversion factor is a ratio used to change one unit of measurement into another. It's essentially a fraction where the numerator and denominator represent the same quantity but in different units. This allows us to cancel out units and arrive at the desired unit of measurement. Mastering conversion factors is crucial in various fields, from chemistry and physics to engineering and everyday life.
Key Characteristics of Conversion Factors:
- Equality: The numerator and denominator are always equal in value, even though they use different units. For example, 1 meter = 100 centimeters, so the conversion factors are 1 m/100 cm and 100 cm/1 m.
- Unit Cancellation: This is the core principle behind using conversion factors. By strategically placing the units, we can cancel out unwanted units and obtain the desired units in the final answer.
- Dimensional Analysis: This technique uses conversion factors to analyze and solve problems involving units. It ensures that the units are consistent throughout the calculation.
Common Conversion Factors
Here are some frequently used conversion factors:
- Metric System: Conversions within the metric system (e.g., meters to centimeters, grams to kilograms, liters to milliliters) are based on powers of 10, making them relatively straightforward.
- Imperial to Metric: Converting between imperial units (e.g., inches, pounds, gallons) and metric units (e.g., centimeters, kilograms, liters) requires specific conversion factors. Examples include:
- 1 inch = 2.54 centimeters
- 1 pound = 0.453592 kilograms
- 1 gallon = 3.78541 liters
- Temperature: Converting between Celsius (°C), Fahrenheit (°F), and Kelvin (K) requires specific formulas:
- °C = (°F - 32) × 5/9
- °F = (°C × 9/5) + 32
- K = °C + 273.15
Problem Solving Strategies using Conversion Factors
Solving problems involving unit conversions often requires a systematic approach. Here's a step-by-step strategy:
- Identify the Given and Required Units: Clearly identify the starting unit and the desired unit.
- Find Relevant Conversion Factors: Determine the necessary conversion factors to bridge the gap between the given and required units. You might need multiple conversion factors for complex problems.
- Set Up the Conversion: Arrange the conversion factors as a chain of fractions, ensuring that unwanted units cancel out. The units should cancel diagonally.
- Perform the Calculation: Multiply the given value by the chain of conversion factors.
- Check the Units and Answer: Ensure that the final units match the desired units. Check the reasonableness of your answer – does it make sense in the context of the problem?
Lab 2 Report Sheet Answers: Common Challenges and Solutions
Lab 2 reports often involve applying conversion factors to experimental data. Here are some common challenges and solutions:
Challenge 1: Incorrect Unit Cancellation
Problem: Students often struggle to correctly arrange conversion factors, leading to incorrect unit cancellation and an erroneous final answer.
Solution: Carefully analyze the units in each step. Ensure that unwanted units cancel diagonally before proceeding to the next step. Rewrite the problem, clearly showing the cancellation of units.
Challenge 2: Multiple Conversion Factors
Problem: Problems requiring multiple conversion factors can be daunting. Students may get lost in the process, leading to errors.
Solution: Break down the problem into smaller, manageable steps. Focus on converting one unit at a time. Visualize the process using a flow chart or diagram to track unit cancellations.
Challenge 3: Significant Figures and Rounding
Problem: Students may struggle with determining the correct number of significant figures in their final answer, leading to inaccurate results.
Solution: Understand the rules of significant figures. Retain the same number of significant figures as the least precise measurement in the problem. Round the final answer to the correct number of significant figures.
Challenge 4: Understanding Scientific Notation
Problem: Working with very large or very small numbers (often encountered in scientific contexts) can be challenging without a grasp of scientific notation.
Solution: Practice converting numbers to and from scientific notation. Use your calculator's scientific notation functions to simplify calculations. Remember that scientific notation facilitates easier manipulation and understanding of very large or very small quantities.
Challenge 5: Interpreting Experimental Data
Problem: Correctly interpreting the data from the lab experiment is crucial for accurate conversion factor application.
Solution: Carefully review the experimental procedure and data collection methods. Understand the units associated with each measurement. Identify any potential sources of error and their impact on the final results. Communicate uncertainties associated with your experimental measurements.
Example Problems and Solutions
Let's illustrate these concepts with some example problems:
Problem 1: Convert 5000 centimeters to kilometers.
Solution:
- Given: 5000 cm
- Required: km
- Conversion factors: 1 m = 100 cm; 1 km = 1000 m
- Setup: 5000 cm × (1 m / 100 cm) × (1 km / 1000 m)
- Calculation: 0.05 km
Problem 2: A rectangular block measures 2.5 inches by 4 inches by 6 inches. What is its volume in cubic centimeters?
Solution:
- Given: 2.5 in, 4 in, 6 in
- Required: cm³
- Conversion factor: 1 in = 2.54 cm
- Calculation: Volume (in³) = 2.5 in × 4 in × 6 in = 60 in³ Volume (cm³) = 60 in³ × (2.54 cm/1 in)³ = 983.2 cm³ (approximately)
Advanced Topics and Considerations
- Uncertainty and Error Analysis: Incorporate error analysis in your calculations and report, addressing potential sources of error and their impact on the final results. This showcases a deeper understanding of the experimental process.
- Data Visualization: Present your results graphically (e.g., bar charts, scatter plots) to enhance clarity and understanding. This visually reinforces your findings.
- Writing a Comprehensive Lab Report: Structure your lab report logically, including an introduction, methods, results, discussion, and conclusion. Clearly present your calculations and analysis.
Conclusion
Mastering conversion factors and applying them effectively in problem-solving is fundamental to success in many scientific and engineering disciplines. By understanding the underlying principles, employing effective strategies, and meticulously analyzing data, you can confidently tackle complex problems and produce high-quality lab reports. Remember to carefully check your units, apply the correct number of significant figures, and present your work clearly and concisely. This comprehensive guide equips you with the necessary knowledge and skills to excel in your lab work and beyond. Remember that consistent practice is key to solidifying your understanding and achieving proficiency in this crucial area of study.
Latest Posts
Latest Posts
-
Software Piracy Include All The Following Except
Mar 30, 2025
-
What Is The Molar Mass Of Co No3 2
Mar 30, 2025
-
Most Electric Gas And Water Companies Are Examples Of
Mar 30, 2025
-
Why Are The Beta Pleated Multimers Of Prp Potentially Pathogenic
Mar 30, 2025
-
Which Of The Following Best Describes The Sympathetic Division
Mar 30, 2025
Related Post
Thank you for visiting our website which covers about Conversion Factors And Problem Solving Lab 2 Report Sheet Answers . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
