Consider The Differential Equation Dy Dx Y 1 X 2
Holbox
May 09, 2025 · 5 min read
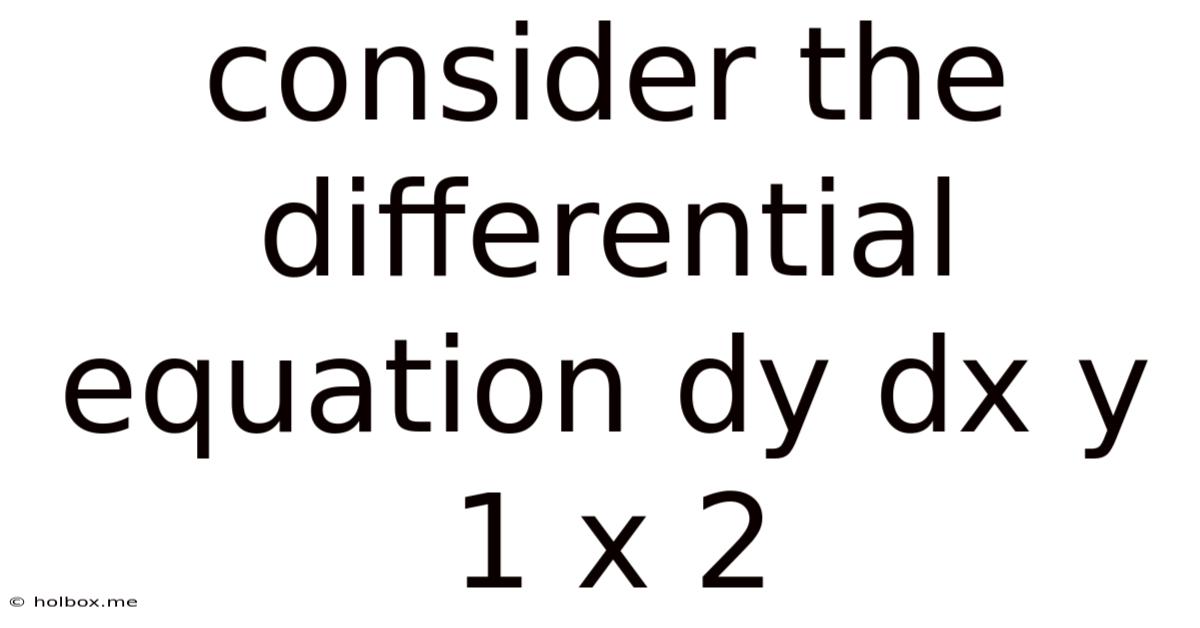
Table of Contents
- Consider The Differential Equation Dy Dx Y 1 X 2
- Table of Contents
- Consider the Differential Equation dy/dx = y/(1 + x²)
- Understanding the Differential Equation
- Identifying the Type of Equation
- Solving the Differential Equation
- Separating the Variables
- Integrating Both Sides
- Solving for y
- Analyzing the Solution
- Alternative Solution Methods
- Applications and Significance
- Conclusion
- Latest Posts
- Related Post
Consider the Differential Equation dy/dx = y/(1 + x²)
The differential equation dy/dx = y/(1 + x²) presents a fascinating case study in understanding and solving ordinary differential equations (ODEs). Its seemingly simple form belies a rich mathematical structure, offering opportunities to explore various solution techniques and analyze the behavior of its solutions. This article delves deep into this equation, examining its properties, solving it using different methods, and exploring the implications of its solutions.
Understanding the Differential Equation
The equation dy/dx = y/(1 + x²) is a first-order, separable ODE. This means it involves only the first derivative of the dependent variable (y) with respect to the independent variable (x), and it can be separated into terms involving only y and only x. This separability is a key characteristic that allows us to directly integrate the equation to find a general solution. The equation describes the relationship between the rate of change of y with respect to x and the values of x and y themselves. This relationship is crucial in numerous applications across various fields, including physics, engineering, and economics.
Identifying the Type of Equation
Understanding the type of differential equation is crucial for selecting the appropriate solution method. As mentioned, this equation is:
- First-order: It involves only the first derivative of y.
- Ordinary: It contains only ordinary derivatives (as opposed to partial derivatives).
- Separable: It can be rewritten in the form dy/dx = f(x)g(y), where f(x) = 1/(1 + x²) and g(y) = y.
This separability allows us to employ a straightforward integration method to find the general solution.
Solving the Differential Equation
The solution process involves separating the variables and then integrating both sides.
Separating the Variables
We begin by separating the variables y and x:
dy/y = dx/(1 + x²)
This separates the equation into a form where each side involves only one variable.
Integrating Both Sides
Now we integrate both sides of the separated equation:
∫ dy/y = ∫ dx/(1 + x²)
The left-hand side integral is a standard integral:
ln|y| = ∫ dx/(1 + x²) + C₁
The right-hand side integral requires the knowledge of a specific integral:
∫ dx/(1 + x²) = arctan(x) + C₂
Therefore, we have:
ln|y| = arctan(x) + C
where C = C₁ + C₂ is the constant of integration.
Solving for y
To solve for y, we exponentiate both sides:
|y| = e^(arctan(x) + C) = e^C * e^(arctan(x))
Since e^C is an arbitrary positive constant, we can replace it with a constant A:
|y| = A * e^(arctan(x))
Removing the absolute value, we get the general solution:
y = ± A * e^(arctan(x))
Finally, we can replace ±A with a new constant K, where K can be any real number:
y = K * e^(arctan(x))
This is the general solution to the differential equation. The constant K represents the family of solutions, each corresponding to a different initial condition.
Analyzing the Solution
The solution y = K * e^(arctan(x)) reveals several key features:
-
Exponential Behavior: The solution exhibits exponential behavior modulated by the arctan(x) function. The arctan(x) function grows slowly, approaching π/2 as x approaches infinity and -π/2 as x approaches negative infinity. This means the exponential term will grow, but at a progressively slower rate.
-
Asymptotic Behavior: As x approaches positive infinity, arctan(x) approaches π/2, so y approaches K * e^(π/2), which is a finite value. Similarly, as x approaches negative infinity, y approaches K * e^(-π/2). Therefore, the solution has horizontal asymptotes.
-
Initial Conditions: The constant K is determined by the initial conditions. Given a specific point (x₀, y₀) that the solution must pass through, we can find the corresponding value of K. For example, if the solution passes through (0, 1), then 1 = K * e^(arctan(0)) = K * e⁰ = K, so K = 1.
Alternative Solution Methods
While the separation of variables method is straightforward in this case, other methods can also be used to solve this differential equation, though they might be less efficient. These include:
-
Integrating Factor Method: Although not directly applicable in its simplest form, the equation could be manipulated to use an integrating factor, but this would involve unnecessary complexity.
-
Numerical Methods: For situations where an analytical solution is difficult or impossible to obtain, numerical methods such as Euler's method or Runge-Kutta methods can approximate the solution. These methods are particularly useful for solving differential equations with complex forms or boundary conditions.
Applications and Significance
This seemingly simple differential equation finds applications in various contexts. While a direct physical interpretation might not be immediately obvious, the form of the equation and its solution can serve as a building block or simplified representation in more complex models. Its properties, such as the asymptotic behavior, are valuable in understanding systems that approach equilibrium or steady-state conditions. For instance, certain models in population dynamics or chemical kinetics might exhibit similar asymptotic trends, though often with more complex governing equations. Furthermore, the techniques used to solve this equation (separation of variables, integration) are fundamental tools in the broader field of differential equations and are applicable to a wide range of more complex problems.
Conclusion
The differential equation dy/dx = y/(1 + x²) offers a valuable opportunity to explore fundamental concepts in solving and analyzing ordinary differential equations. Its solution, y = K * e^(arctan(x)), showcases the interplay between exponential and trigonometric functions, resulting in solutions with well-defined asymptotic behavior. The methods employed, particularly the separation of variables, are essential tools in the mathematician's arsenal. Understanding the behavior of this equation provides a solid foundation for tackling more complex differential equations encountered in diverse fields of science and engineering. The simplicity of this particular example allows for a deeper appreciation of the underlying mathematical principles without being overshadowed by the complexities that often arise in more applied contexts.
Latest Posts
Related Post
Thank you for visiting our website which covers about Consider The Differential Equation Dy Dx Y 1 X 2 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.