Complete The Synthetic Division Problem Below 2 1 5
Holbox
Mar 25, 2025 · 5 min read
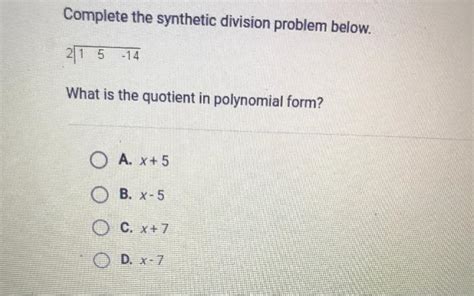
Table of Contents
- Complete The Synthetic Division Problem Below 2 1 5
- Table of Contents
- Mastering Synthetic Division: A Comprehensive Guide to Solving 2 | 1 | 5
- Understanding the Basics of Synthetic Division
- What is Synthetic Division?
- When to Use Synthetic Division
- The Setup: Coefficients and the Divisor
- Solving the Problem: 2 | 1 | 5
- Step-by-Step Solution:
- Interpreting the Results
- Expanding the Application: More Complex Examples
- Example 1: Dividing a Cubic Polynomial
- Example 2: Handling Missing Terms
- Advanced Applications of Synthetic Division
- Finding Polynomial Roots
- Evaluating Polynomials (Remainder Theorem)
- Partial Fraction Decomposition
- Error Handling and Common Mistakes
- Conclusion: Mastering Synthetic Division
- Latest Posts
- Latest Posts
- Related Post
Mastering Synthetic Division: A Comprehensive Guide to Solving 2 | 1 | 5
Synthetic division is a simplified method for dividing polynomials, particularly useful when the divisor is a linear expression (x - c). While long division offers a more general approach, synthetic division's efficiency makes it a preferred technique for many polynomial division problems. This guide provides a comprehensive understanding of synthetic division, walking you through the process, explaining the underlying principles, and offering advanced applications. We'll also tackle the specific problem: 2 | 1 | 5.
Understanding the Basics of Synthetic Division
Before diving into the specific problem, let's establish a solid foundation in the mechanics and theory behind synthetic division.
What is Synthetic Division?
Synthetic division is a shorthand method for performing polynomial long division. It streamlines the process by focusing only on the coefficients of the polynomials, omitting the variables and their powers. This makes the calculation significantly faster and less prone to errors.
When to Use Synthetic Division
Synthetic division is best suited for dividing a polynomial by a linear factor of the form (x - c), where 'c' is a constant. If your divisor is anything more complex than a linear expression (e.g., a quadratic or higher-degree polynomial), long division is necessary.
The Setup: Coefficients and the Divisor
The critical step is setting up the problem correctly. You'll need the coefficients of the dividend (the polynomial being divided) arranged in descending order of powers, including zeros for any missing terms. The divisor, (x - c), provides the value 'c', which will be placed outside the synthetic division bracket.
Solving the Problem: 2 | 1 | 5
Now, let's address the specific problem presented: 2 | 1 | 5. This implies we're dividing a polynomial with coefficients 1 and 5 by the linear factor (x - 2).
Step-by-Step Solution:
-
Setup: Write the divisor (2) to the left and the coefficients (1 and 5) in a row to the right, separated by a line. Since there's only two coefficients, this would imply that we are dividing a polynomial with the highest power of 1.
2 | 1 5 -
Bring Down the First Coefficient: Bring down the first coefficient (1) without any alteration.
2 | 1 5 1 -
Multiply and Add: Multiply the value outside the bracket (2) by the number you just brought down (1). This gives 2. Write this result under the second coefficient (5). Add the two numbers together. 5 + 2 = 7.
2 | 1 5 1 2 --- 7 -
The Result: The final row of numbers (1 and 7) represents the coefficients of the quotient polynomial. The last number (7) is the remainder.
Therefore, the solution to 2 | 1 | 5 is:
- Quotient: x + 7
- Remainder: 0
Interpreting the Results
The result tells us that the polynomial represented by the coefficients 1 and 5, which is x + 5, divided by (x - 2) results in a quotient of x + 7. Therefore, we can express this relationship as:
x + 5 = (x - 2)(x + 7)
Expanding the Application: More Complex Examples
Let's explore synthetic division with more elaborate polynomials to solidify your understanding.
Example 1: Dividing a Cubic Polynomial
Consider the polynomial 2x³ + 5x² - 8x + 3, which we want to divide by (x - 1).
-
Setup: Arrange the coefficients: 2 | 5 | -8 | 3
-
Step-by-Step:
1 | 2 5 -8 3 | 2 7 -1 ----------------- 2 7 -1 2 -
Result: The quotient is 2x² + 7x - 1, and the remainder is 2.
Example 2: Handling Missing Terms
Let's say we need to divide 3x⁴ - 2x² + 5 by (x + 2). Note the absence of the x³ and x terms. We must include zeros as placeholders for these missing terms.
-
Setup: Remember that (x + 2) means c = -2. The coefficients become: -2 | 3 | 0 | -2 | 0 | 5
-
Step-by-Step:
-2 | 3 0 -2 0 5 | -6 12 -20 40 -------------------- 3 -6 10 -20 45 -
Result: The quotient is 3x³ - 6x² + 10x - 20, and the remainder is 45.
Advanced Applications of Synthetic Division
Beyond basic polynomial division, synthetic division offers valuable applications in:
Finding Polynomial Roots
If the remainder after synthetic division is 0, it means the divisor is a factor of the polynomial. This is a powerful tool for finding roots (solutions) of polynomial equations. If a root is found using this technique, you can further factor the resulting polynomial.
Evaluating Polynomials (Remainder Theorem)
The Remainder Theorem states that when a polynomial P(x) is divided by (x - c), the remainder is P(c). This means we can use synthetic division to efficiently evaluate a polynomial at a specific value. This can be particularly helpful when the polynomial is of higher order.
Partial Fraction Decomposition
In calculus, partial fraction decomposition is a critical technique for integrating rational functions. Synthetic division can simplify the process of finding the coefficients of the partial fractions.
Error Handling and Common Mistakes
While synthetic division is efficient, it's crucial to avoid common errors:
- Incorrect coefficient placement: Double-check the coefficients of your dividend for accuracy and ensure you include zeros for any missing terms.
- Arithmetic errors: Carefully perform the multiplication and addition steps to avoid simple calculation mistakes.
- Misinterpreting the result: Always correctly identify the quotient and the remainder, recognizing the role of the last number in the final row.
Conclusion: Mastering Synthetic Division
Synthetic division, although a seemingly simple technique, provides a highly efficient means for polynomial division when the divisor is linear. Mastering this method enhances your understanding of polynomials, aids in finding roots, evaluating functions, and proves invaluable in more advanced mathematical contexts. By diligently practicing the steps outlined, understanding the underlying principles, and exercising caution in avoiding common errors, you'll develop the proficiency needed to seamlessly solve diverse polynomial division problems. Remember, consistent practice is key to building your expertise and confidence in mastering this essential mathematical tool.
Latest Posts
Latest Posts
-
The Pth Percentile Is A Value Such That Approximately
Mar 27, 2025
-
Where Are You Allowed To Wash Your Hands
Mar 27, 2025
-
Finally What Is The Numerical Vaue Of A
Mar 27, 2025
-
According To The Text Private Prep Schools Are Believed To
Mar 27, 2025
-
Per Capita Gdp Will Rise If Gdp
Mar 27, 2025
Related Post
Thank you for visiting our website which covers about Complete The Synthetic Division Problem Below 2 1 5 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
