Approximate Using The Contour Diagram Of Shown Below.
Holbox
Mar 28, 2025 · 5 min read
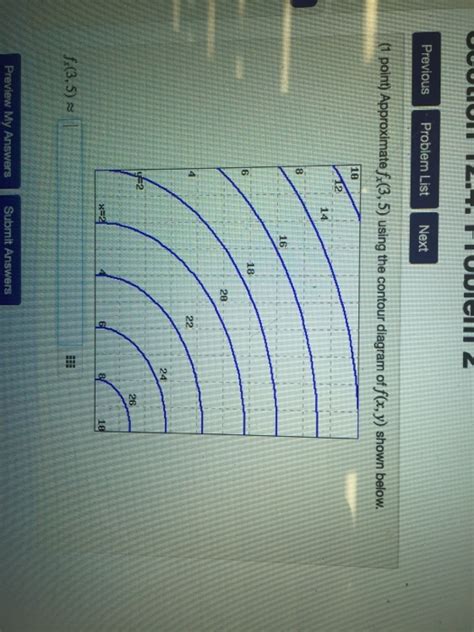
Table of Contents
- Approximate Using The Contour Diagram Of Shown Below.
- Table of Contents
- Approximating Values Using Contour Diagrams: A Comprehensive Guide
- Understanding Contour Diagrams
- Key Features of Contour Diagrams:
- Approximating Values: Basic Techniques
- Linear Interpolation: Improving Accuracy
- Advanced Approximation Techniques
- Using Gradient Information
- Numerical Methods for Interpolation
- Practical Applications of Contour Diagram Approximation
- Geography and Cartography:
- Engineering and Physics:
- Economics and Finance:
- Limitations of Contour Diagram Approximation
- Enhancing Accuracy: Tips and Considerations
- Conclusion: Mastering Contour Diagram Approximation
- Latest Posts
- Latest Posts
- Related Post
Approximating Values Using Contour Diagrams: A Comprehensive Guide
Contour diagrams, also known as contour maps or level curves, are powerful visual tools used to represent three-dimensional surfaces in two dimensions. They display curves connecting points of equal value of a function, providing a concise way to understand the function's behavior across its domain. This article delves into the techniques and strategies for approximating values using contour diagrams, exploring various scenarios and emphasizing practical applications. We'll cover everything from basic interpretation to more advanced approximation methods, ensuring you gain a thorough understanding of this valuable analytical tool.
Understanding Contour Diagrams
Before diving into approximation techniques, let's solidify our understanding of contour diagrams. Imagine a hilly landscape. A contour line on a topographic map represents a line of constant elevation. Similarly, in a contour diagram for a mathematical function, z = f(x, y), each contour line connects points (x, y) where the function f(x, y) has the same value. These values are often labelled on the diagram.
Key Features of Contour Diagrams:
- Contour Lines: These are the curves connecting points of equal value. Closely spaced contour lines indicate a steep change in the function's value, while widely spaced lines suggest a gentler slope.
- Contour Intervals: The difference in value between consecutive contour lines. A consistent contour interval simplifies interpretation.
- Labels: Numerical labels on contour lines indicate the function's value along that line.
- Gradient: The direction of the steepest ascent is always perpendicular to the contour lines.
Approximating Values: Basic Techniques
The simplest method for approximating values using a contour diagram involves visually locating the point of interest and determining the closest contour line. The value of that contour line provides a reasonable approximation. However, this approach yields a relatively coarse approximation.
Linear Interpolation: Improving Accuracy
For a more accurate approximation, we can employ linear interpolation. This technique assumes a linear relationship between the function's values along the contour lines. Let's consider a scenario where we need to approximate the value of f(x, y) at a point P that lies between two contour lines with values z₁ and z₂.
- Identify the Contour Lines: Determine the two contour lines that bracket point P.
- Estimate the Proportions: Visually estimate the proportional distance of P between these two contour lines. Let's say P is k proportion of the distance from the z₁ contour to the z₂ contour, where 0 ≤ k ≤ 1.
- Apply Linear Interpolation: The approximated value z at point P can be calculated using the formula: z = z₁ + k(z₂ - z₁).
This method provides a significantly improved approximation compared to simply identifying the closest contour line.
Advanced Approximation Techniques
While linear interpolation is useful, it assumes linearity between contour lines, which might not always hold true, especially when dealing with complex functions or steeply changing gradients. In such cases, more sophisticated methods can provide better accuracy.
Using Gradient Information
Contour diagrams implicitly provide information about the function's gradient. Remember, the gradient is perpendicular to the contour lines and points in the direction of the steepest ascent. By analyzing the spacing and orientation of contour lines near the point of interest, we can gain insights into the gradient's magnitude and direction. This qualitative information can refine our approximation, particularly when combined with linear interpolation.
Numerical Methods for Interpolation
For highly accurate approximation, particularly when dealing with densely packed contour lines or complex functions, numerical methods like bilinear interpolation or higher-order interpolation techniques can be employed. These techniques consider the values at multiple neighboring points, providing a more refined and accurate estimate. However, they generally require more computational effort and are often best implemented using software tools.
Practical Applications of Contour Diagram Approximation
Contour diagrams find widespread applications across diverse scientific and engineering fields:
Geography and Cartography:
- Elevation modeling: Topographic maps use contour lines to represent elevation, enabling the approximation of heights at specific locations.
- Weather mapping: Contour maps depict weather patterns like temperature, pressure, and precipitation, allowing for the approximation of weather conditions at specific points.
Engineering and Physics:
- Fluid dynamics: Contour diagrams visualize pressure, velocity, and temperature distributions in fluid flows, aiding in the approximation of these parameters at specific points.
- Electromagnetism: Contour diagrams illustrate electric and magnetic fields, enabling the approximation of field strengths at various locations.
- Heat transfer: Contour maps show temperature distributions in heat transfer problems, enabling the approximation of temperatures at various points in a system.
Economics and Finance:
- Utility functions: Contour diagrams depict indifference curves in economics, enabling the approximation of utility levels for different consumption bundles.
- Risk analysis: Contour maps can visually represent risk levels associated with different investment strategies, aiding in decision-making.
Limitations of Contour Diagram Approximation
It's crucial to acknowledge the limitations inherent in approximating values from contour diagrams:
- Resolution: The accuracy of approximation is directly limited by the resolution of the contour diagram; a coarser diagram leads to less accurate approximations.
- Interpolation Assumptions: Linear interpolation, while generally accurate, assumes linearity between contour lines, which might not always be true.
- Visual Interpretation: The accuracy of the approximation also depends on the accuracy of visual interpretation; subjective judgment can introduce errors.
Enhancing Accuracy: Tips and Considerations
To improve the accuracy of your approximations:
- Choose a diagram with appropriate resolution: Select a diagram with closely spaced contour lines, especially in regions of steep gradients.
- Use appropriate interpolation methods: Linear interpolation is sufficient for many cases; however, more advanced techniques can provide improved accuracy when needed.
- Consider the context: Understand the limitations of the data represented in the contour diagram.
- Employ multiple techniques: Combine visual inspection with interpolation techniques to enhance accuracy and minimize errors.
Conclusion: Mastering Contour Diagram Approximation
Contour diagrams provide a powerful and visually intuitive way to represent complex functions. Mastering the techniques of approximation from these diagrams is invaluable across various disciplines. By understanding the basics, employing appropriate interpolation methods, and acknowledging inherent limitations, you can accurately approximate values and unlock the full potential of contour diagrams as a tool for analysis and interpretation. This comprehensive guide has equipped you with the knowledge and strategies to confidently navigate the world of contour diagram approximation, enabling you to extract valuable insights from this versatile visual representation of functional data. Remember to always consider the context, limitations, and available techniques to achieve the most accurate and reliable approximations.
Latest Posts
Latest Posts
-
Final Goods And Services Refer To
Apr 01, 2025
-
A Decrease In The Interest Rate Will
Apr 01, 2025
-
Which Statements Reflect A Servant Leadership Mindset
Apr 01, 2025
-
Which Of The Following Describes The Plasma Membrane
Apr 01, 2025
-
Draw The Product Of The Hydration Of 2 Butene
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about Approximate Using The Contour Diagram Of Shown Below. . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
