A Carnot Refrigerator Absorbs Heat From A Space At 15
Holbox
Mar 31, 2025 · 5 min read
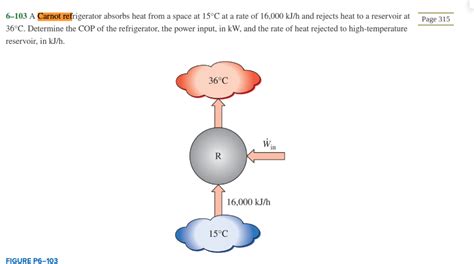
Table of Contents
- A Carnot Refrigerator Absorbs Heat From A Space At 15
- Table of Contents
- A Carnot Refrigerator Absorbing Heat from a Space at 15°C: A Deep Dive into Thermodynamics
- Understanding the Carnot Cycle in a Refrigerator
- 1. Isothermal Expansion (Heat Absorption):
- 2. Adiabatic Expansion:
- 3. Isothermal Compression (Heat Rejection):
- 4. Adiabatic Compression:
- Calculating the Coefficient of Performance (COP)
- Factors Affecting the COP of a Carnot Refrigerator
- 1. Temperature Difference:
- 2. Reversibility:
- 3. Refrigerant Properties:
- 4. Heat Transfer Mechanisms:
- Comparison with Real-World Refrigerators
- Implications and Applications
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
A Carnot Refrigerator Absorbing Heat from a Space at 15°C: A Deep Dive into Thermodynamics
The Carnot refrigerator, a theoretical marvel of thermodynamics, provides a benchmark for understanding the limits of refrigeration efficiency. This article will delve into the intricacies of a Carnot refrigerator absorbing heat from a space maintained at a constant 15°C (288.15 K), exploring its operation, efficiency, and implications for real-world refrigeration systems. We will cover various aspects, including the Carnot cycle, its limitations, and practical considerations.
Understanding the Carnot Cycle in a Refrigerator
The Carnot refrigerator operates on a reversed Carnot cycle, a thermodynamic cycle consisting of four reversible processes:
1. Isothermal Expansion (Heat Absorption):
The refrigerant, typically a gas, absorbs heat from the low-temperature reservoir (15°C in our case) at a constant temperature. This process increases the refrigerant's internal energy and volume. The heat absorbed is denoted as Qc (where 'c' stands for cold reservoir). This is where the cooling effect happens. The refrigerator absorbs heat from the space it is meant to cool down.
2. Adiabatic Expansion:
The refrigerant then expands adiabatically, meaning no heat exchange occurs with the surroundings. This expansion causes a further decrease in the refrigerant's temperature. The temperature drop is crucial for efficient cooling. The work done by the refrigerant during this expansion is crucial to the entire process.
3. Isothermal Compression (Heat Rejection):
The refrigerant, now at a lower temperature, is compressed isothermally at the high-temperature reservoir. During this process, it rejects heat, Qh (where 'h' stands for hot reservoir), to the surroundings. This is the heat that needs to be dissipated, often done through condenser coils.
4. Adiabatic Compression:
Finally, the refrigerant is compressed adiabatically, returning it to its initial state, ready to begin the cycle anew. This process increases the refrigerant's temperature and pressure.
Calculating the Coefficient of Performance (COP)
The efficiency of a refrigerator is not measured by efficiency, but rather by its Coefficient of Performance (COP). Unlike a heat engine, which aims for high efficiency, a refrigerator's goal is to maximize the amount of heat removed from the cold reservoir for a given amount of work input. The COP is defined as:
COP = Qc / W
where:
- Qc is the heat absorbed from the cold reservoir.
- W is the work done on the refrigerant.
For a Carnot refrigerator, the COP can be expressed in terms of the absolute temperatures of the hot and cold reservoirs (Th and Tc respectively):
COP_Carnot = Tc / (Th - Tc)
Let's consider a scenario where the hot reservoir temperature (Th) is 25°C (298.15 K). Then:
COP_Carnot = 288.15 K / (298.15 K - 288.15 K) = 28.815
This means that for every joule of work done on the refrigerant, the Carnot refrigerator can remove 28.815 joules of heat from the 15°C space. This is a theoretical maximum; real-world refrigerators will have lower COP values due to irreversibilities.
Factors Affecting the COP of a Carnot Refrigerator
Several factors influence the COP of a Carnot refrigerator, and understanding these is key to optimizing its performance:
1. Temperature Difference:
The COP is inversely proportional to the temperature difference between the hot and cold reservoirs. A smaller temperature difference leads to a higher COP. In our example, reducing the ambient temperature (Th) or increasing the cold reservoir temperature (Tc) will improve the COP. However, practical limitations exist for Tc as it's dependent on the intended application.
2. Reversibility:
The Carnot refrigerator assumes reversible processes, an idealization. Real-world refrigerators experience irreversibilities such as friction, heat transfer across finite temperature differences, and throttling processes. These reduce the COP significantly.
3. Refrigerant Properties:
The choice of refrigerant influences the COP. Ideally, a refrigerant should have high heat capacity, low viscosity, and good thermal conductivity to facilitate efficient heat transfer. The working fluid is crucial. Different refrigerants have differing thermodynamic properties.
4. Heat Transfer Mechanisms:
Efficient heat transfer between the refrigerant and the hot and cold reservoirs is crucial. This requires effective heat exchangers (like condensers and evaporators) with large surface areas and good heat transfer coefficients. Poorly designed heat exchangers diminish the COP.
Comparison with Real-World Refrigerators
It's important to understand that the Carnot refrigerator is a theoretical model. Real-world refrigerators deviate from this ideal due to irreversibilities and practical constraints. Real refrigerators employ various refrigeration cycles, such as the vapor-compression cycle, which, while less efficient than the Carnot cycle, are more practical to implement.
The COP of a typical household refrigerator is much lower than the theoretical Carnot COP, often ranging from 3 to 5. This difference highlights the challenges in achieving perfect reversibility and minimizing losses in real-world systems.
Implications and Applications
Understanding the Carnot refrigerator's principles is crucial for several reasons:
-
Setting a benchmark: The Carnot COP provides an upper limit on the efficiency of any refrigeration system operating between the same temperature limits. It serves as a standard against which real systems can be compared.
-
Optimizing design: Engineers use the Carnot cycle as a theoretical framework to optimize the design of real-world refrigerators, aiming to minimize irreversibilities and approach the Carnot efficiency as closely as possible.
-
Developing new technologies: Research in advanced refrigeration technologies often focuses on reducing irreversibilities and improving heat transfer to approach the Carnot efficiency. This includes exploring new refrigerants, advanced heat exchanger designs, and innovative thermodynamic cycles.
-
Energy efficiency: Improving the efficiency of refrigeration systems, whether through improved designs or the adoption of more efficient refrigerants, has significant implications for energy conservation and reducing environmental impact.
Conclusion
The Carnot refrigerator, while a theoretical construct, offers invaluable insights into the fundamental principles of refrigeration. By understanding the Carnot cycle, its limitations, and the factors affecting its COP, we can better appreciate the challenges involved in designing efficient refrigeration systems. The COP of 28.815 calculated for our example, while unattainable in practice, provides a powerful benchmark for evaluating the performance of real-world refrigerators. Continuous improvements in refrigeration technology strive to minimize energy consumption, reduce environmental impact, and approach the theoretical ideal set by the Carnot refrigerator. The pursuit of greater efficiency remains a key area of ongoing research and development in this critical field.
Latest Posts
Latest Posts
-
An Annual Ring Is Composed Of Wood And Wood
Apr 03, 2025
-
When A Corporation Pays A Note Payable And Interest
Apr 03, 2025
-
Analyze The Fxip Screen Based On The Data Shown
Apr 03, 2025
-
Which Of The Following Statements About Dynamics Is Correct
Apr 03, 2025
-
A Statue Is Crated And Moved For Cleaning
Apr 03, 2025
Related Post
Thank you for visiting our website which covers about A Carnot Refrigerator Absorbs Heat From A Space At 15 . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
