A 78 Confidence Interval For A Proportion
Holbox
Mar 29, 2025 · 6 min read
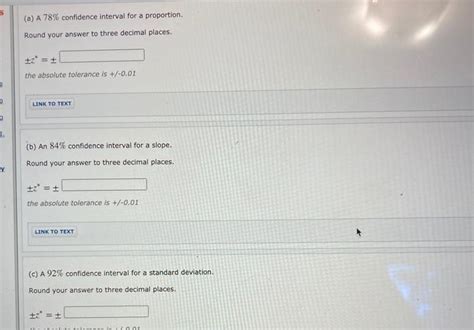
Table of Contents
- A 78 Confidence Interval For A Proportion
- Table of Contents
- A 78% Confidence Interval for a Proportion: A Deep Dive
- What is a Confidence Interval?
- Calculating a 78% Confidence Interval for a Proportion
- Determining the Z-score
- Example Calculation
- Interpreting the 78% Confidence Interval
- Choosing the Appropriate Confidence Level
- Comparing 78% and 95% Confidence Intervals
- Sample Size Considerations
- Limitations of Confidence Intervals
- Conclusion
- Latest Posts
- Latest Posts
- Related Post
A 78% Confidence Interval for a Proportion: A Deep Dive
Understanding confidence intervals is crucial for anyone working with statistical data. While 95% confidence intervals are commonly used, a 78% confidence interval offers a different perspective, potentially useful in situations where a higher level of risk is acceptable or where the sample size is limited. This article provides a comprehensive guide to constructing and interpreting a 78% confidence interval for a proportion, exploring its nuances and applications.
What is a Confidence Interval?
A confidence interval is a range of values that is likely to contain the true value of a population parameter. In simpler terms, imagine you're trying to estimate the percentage of people who prefer coffee over tea. You can't survey everyone, so you take a sample and calculate the percentage in your sample. A confidence interval provides a range around this sample percentage, indicating where the true population percentage likely falls.
The confidence level, in this case, 78%, signifies the percentage of times that the interval constructed from a large number of independent samples would contain the true population proportion. A 78% confidence interval means that if you were to repeat your sampling and interval calculation many times, 78% of these intervals would encompass the true population proportion. It doesn't mean there's a 78% chance the true proportion lies within this particular interval; the true proportion either lies within the interval or it doesn't.
Calculating a 78% Confidence Interval for a Proportion
The formula for calculating a confidence interval for a proportion is relatively straightforward:
CI = p ± Z * √[(p * (1-p)) / n]
Where:
- CI is the confidence interval.
- p is the sample proportion (the number of successes divided by the sample size).
- Z is the Z-score corresponding to the desired confidence level.
- n is the sample size.
Determining the Z-score
The crucial difference between a 78% confidence interval and a more common 95% interval lies in the Z-score. The Z-score represents the number of standard deviations from the mean. To find the Z-score for a 78% confidence level:
- Find the alpha level (α): α = 1 - Confidence Level = 1 - 0.78 = 0.22
- Divide alpha by 2: α/2 = 0.22 / 2 = 0.11
- Find the corresponding Z-score: Use a Z-table or statistical calculator to find the Z-score that corresponds to a cumulative probability of 1 - α/2 = 1 - 0.11 = 0.89. This Z-score will be approximately 1.23. Remember that the Z-score is positive because we are looking at the upper tail of the distribution. The lower bound will use a Z-score of -1.23.
Example Calculation
Let's say we conducted a survey of 500 people (n = 500) and found that 300 (p = 300/500 = 0.6) prefer coffee over tea. To calculate the 78% confidence interval:
- Calculate the standard error: √[(0.6 * (1-0.6)) / 500] ≈ 0.0219
- Calculate the margin of error: 1.23 * 0.0219 ≈ 0.0269
- Calculate the confidence interval: 0.6 ± 0.0269 = (0.5731, 0.6269)
Therefore, we can say with 78% confidence that the true population proportion of people who prefer coffee over tea lies between 57.31% and 62.69%.
Interpreting the 78% Confidence Interval
The interpretation of a 78% confidence interval is crucial and often misunderstood. It does not mean there's a 78% probability that the true population proportion lies within the calculated interval. The true proportion is either within the interval or it isn't.
Instead, the 78% signifies the long-run reliability of the method. If you were to repeat this survey and calculation many times, approximately 78% of the resulting confidence intervals would contain the true population proportion. The remaining 22% would not, due to sampling variability.
Choosing the Appropriate Confidence Level
The choice of confidence level (78% in this case) depends on the context and the acceptable level of risk. A lower confidence level like 78% results in a narrower interval compared to a higher confidence level like 95%. A narrower interval provides a more precise estimate, but it also increases the risk of missing the true population proportion.
A 78% confidence interval might be appropriate when:
- Resource constraints: A larger sample size is needed for higher confidence levels. If resources are limited, a lower confidence level might be acceptable to obtain a reasonable estimate.
- Preliminary analysis: A 78% confidence interval can be used for initial exploration of data before committing to a more extensive study requiring higher confidence.
- Risk tolerance: In situations where a slightly higher risk of missing the true value is acceptable, a lower confidence level can be used. For example, in marketing analysis, a 78% confidence interval might be sufficient to guide decision-making when the cost of missing the true value isn't excessively high.
Comparing 78% and 95% Confidence Intervals
The key difference lies in the margin of error and the Z-score. A 95% confidence interval will have a larger Z-score (approximately 1.96) and thus a wider margin of error, leading to a wider interval. This wider interval reflects the increased confidence that the true population proportion falls within that range. A 78% confidence interval, with its smaller Z-score, produces a narrower interval, offering a more precise estimate but at the cost of reduced confidence.
The choice between 78% and 95% depends heavily on the specific application and the consequences of being wrong. In situations where a precise but less certain estimate is acceptable, a 78% interval might be sufficient. However, for crucial decisions with potentially significant consequences, a higher confidence level like 95% is generally preferred.
Sample Size Considerations
The sample size significantly impacts the width of the confidence interval, regardless of the confidence level. Larger sample sizes lead to narrower intervals, providing more precise estimates. This is true for both 78% and 95% confidence intervals. The formula for calculating the sample size required for a specified margin of error and confidence level involves the Z-score and the estimated population proportion. A larger sample size is required for higher confidence levels or smaller margins of error.
Limitations of Confidence Intervals
It's crucial to acknowledge that confidence intervals have limitations:
- Assumptions: The calculations assume a random sample and a sufficiently large sample size. Violating these assumptions can lead to inaccurate intervals.
- Population variability: The width of the interval is affected by the variability within the population. Highly variable populations will require larger sample sizes for narrower intervals.
- Interpretation: The common misinterpretation of the confidence level needs to be emphasized. It's the reliability of the method, not the probability of the true value being within a specific interval.
Conclusion
A 78% confidence interval provides a valuable tool for estimating population proportions when a slightly higher risk of error is acceptable compared to a 95% confidence interval. By understanding the calculation, interpretation, and limitations of this method, researchers and analysts can make informed decisions based on their data and risk tolerance. While 95% remains the gold standard in many applications, understanding the flexibility of adjusting the confidence level allows for tailoring statistical analysis to specific needs and contexts. Remember to always carefully consider the implications of choosing a lower confidence level and ensure it aligns appropriately with the research objectives and potential consequences.
Latest Posts
Latest Posts
-
Developing Person Through Childhood And Adolescence
Apr 01, 2025
-
The Following Picture Would Be Best Described As
Apr 01, 2025
-
Match Each Term With The Correct Definition
Apr 01, 2025
-
Match These Prefixes Suffixes And Roots To Their Meanings
Apr 01, 2025
-
Match The Bone With The Region It Comes From
Apr 01, 2025
Related Post
Thank you for visiting our website which covers about A 78 Confidence Interval For A Proportion . We hope the information provided has been useful to you. Feel free to contact us if you have any questions or need further assistance. See you next time and don't miss to bookmark.
